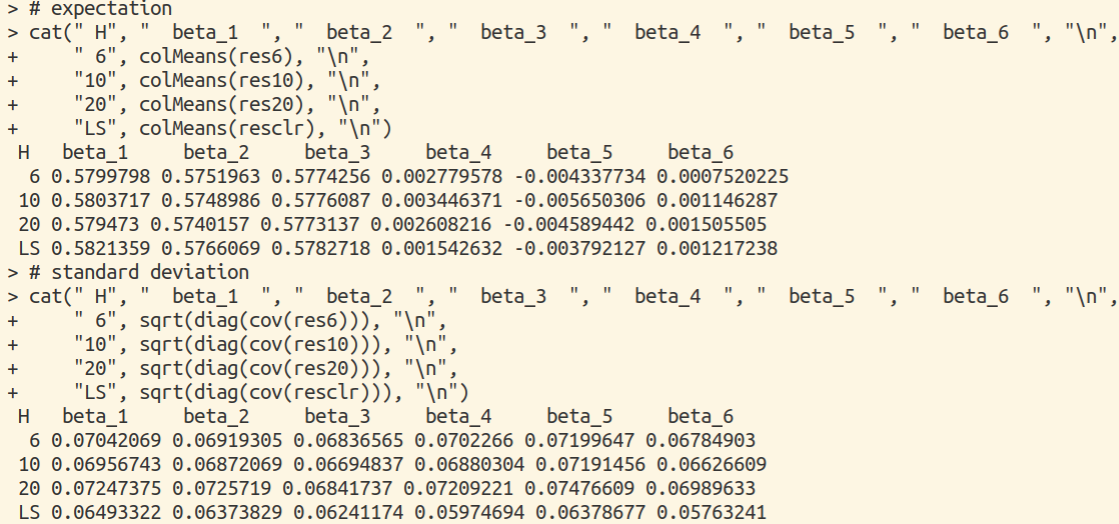
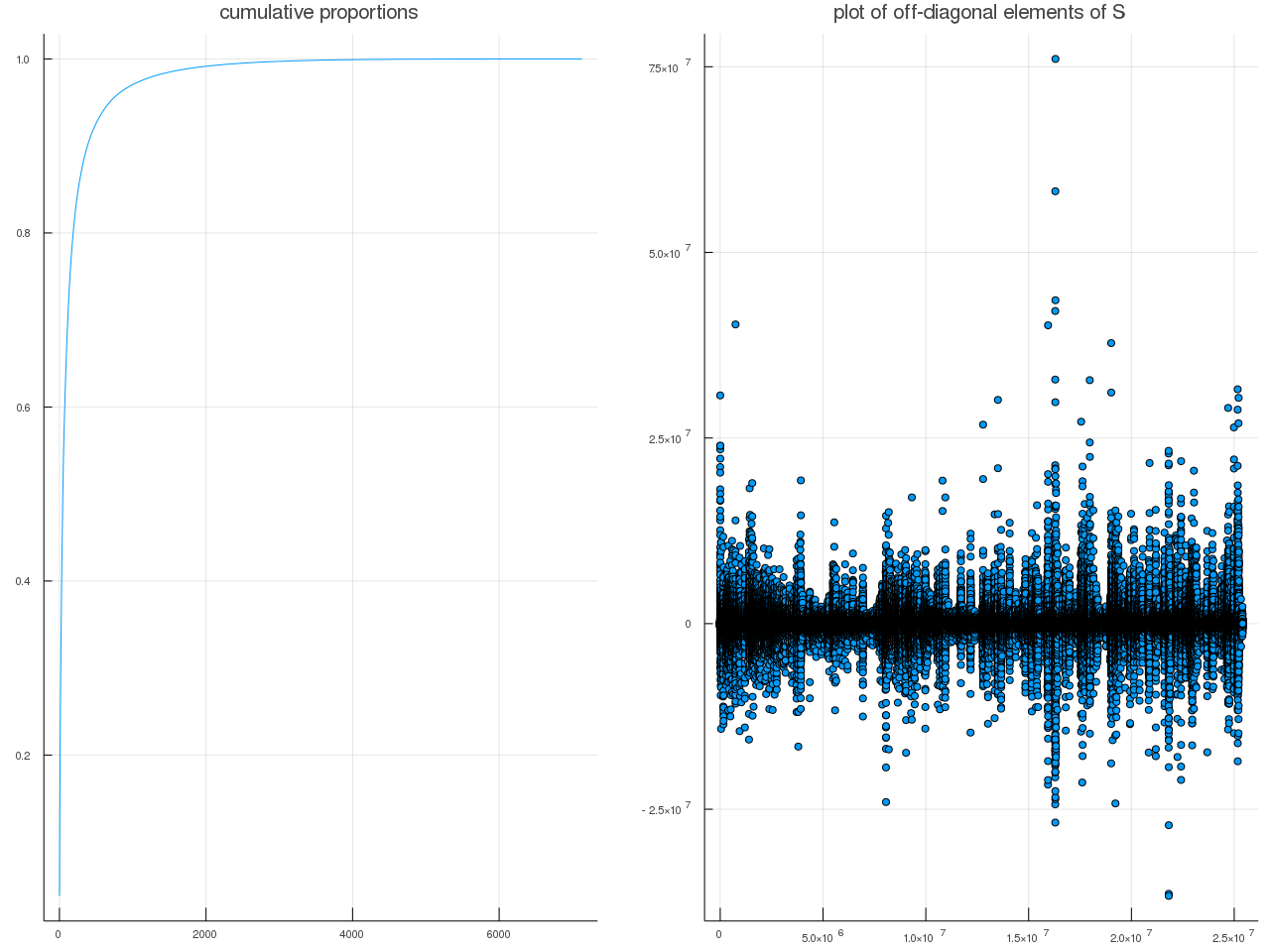
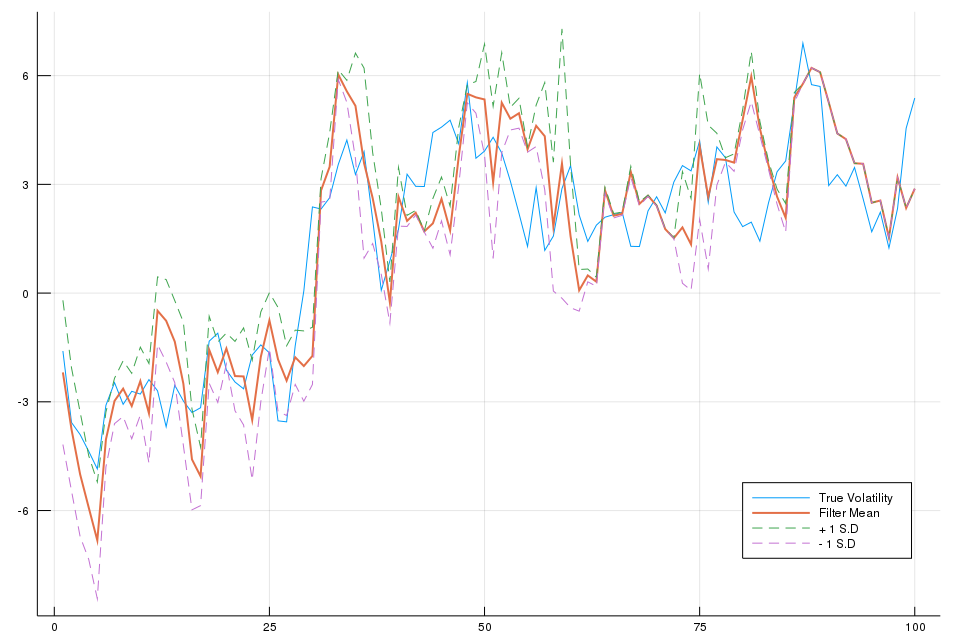
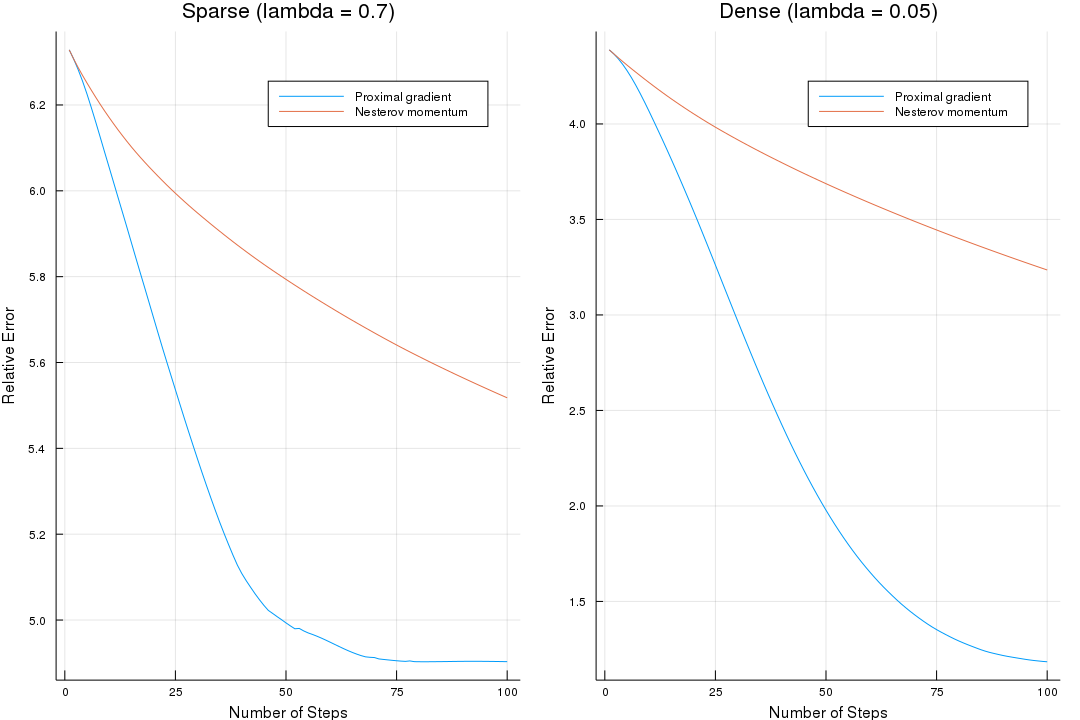
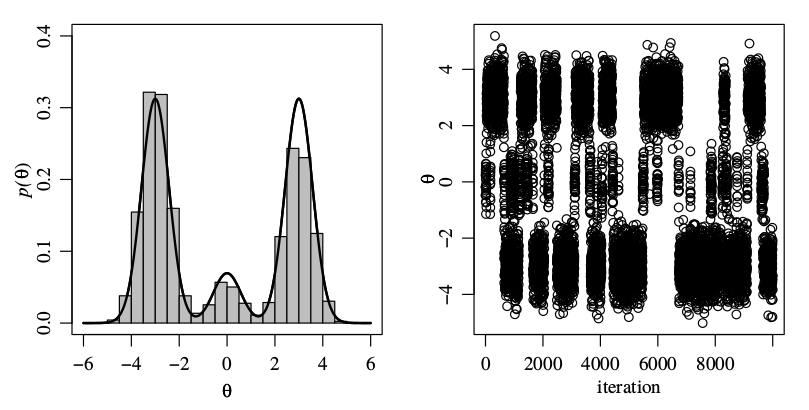
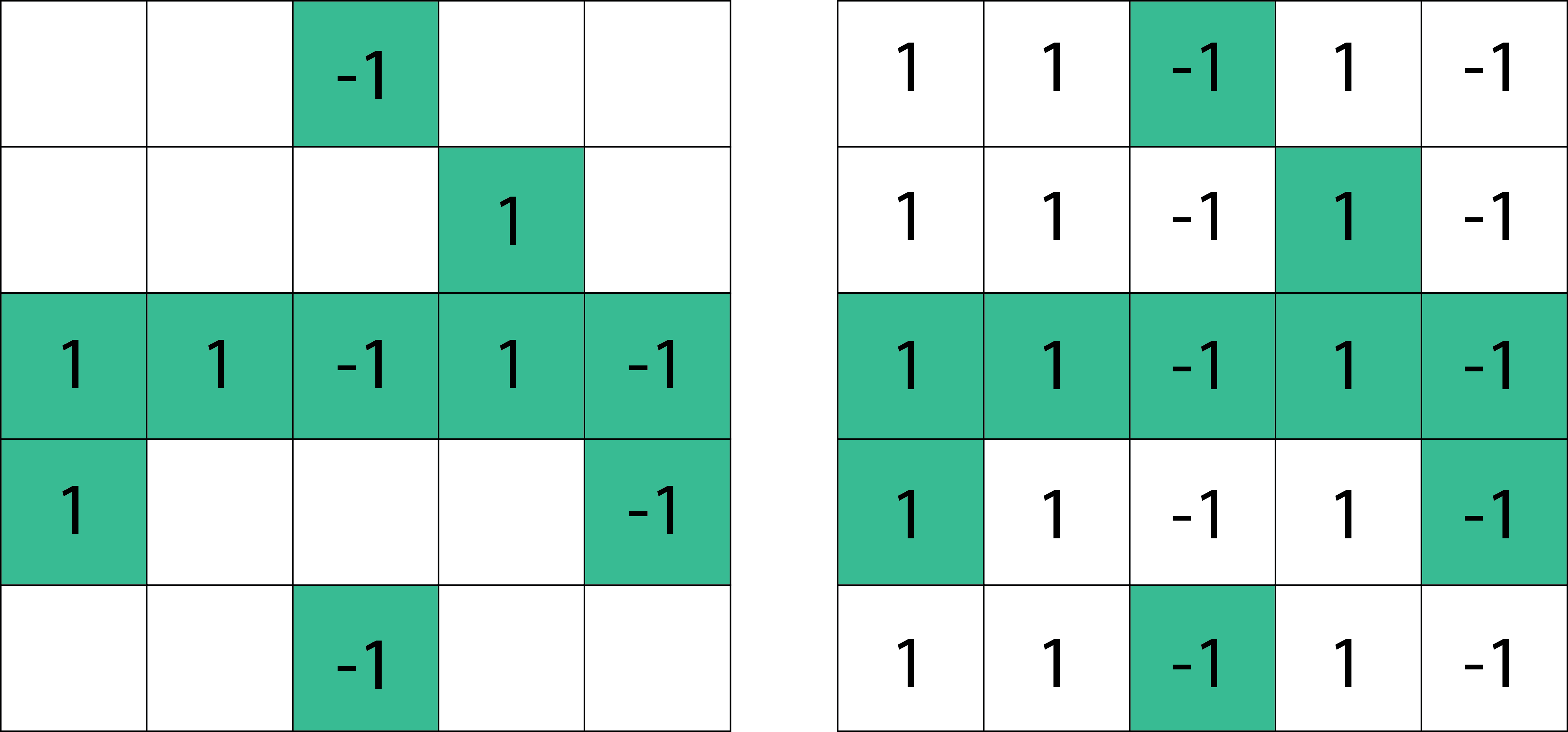
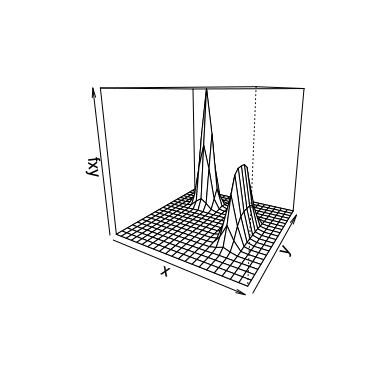
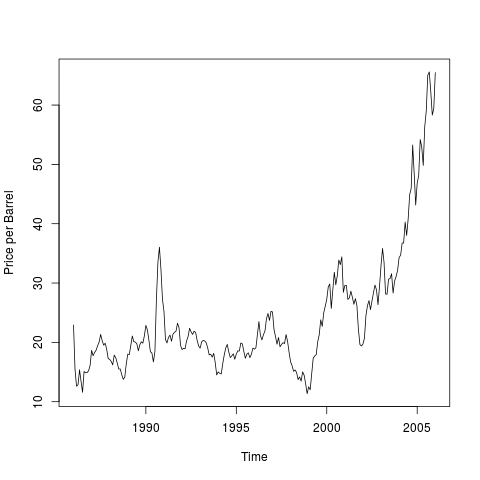
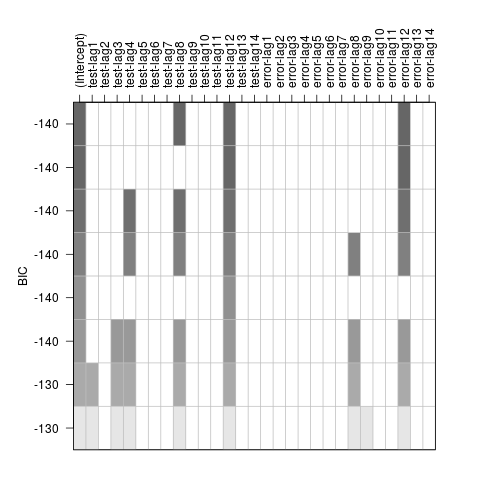
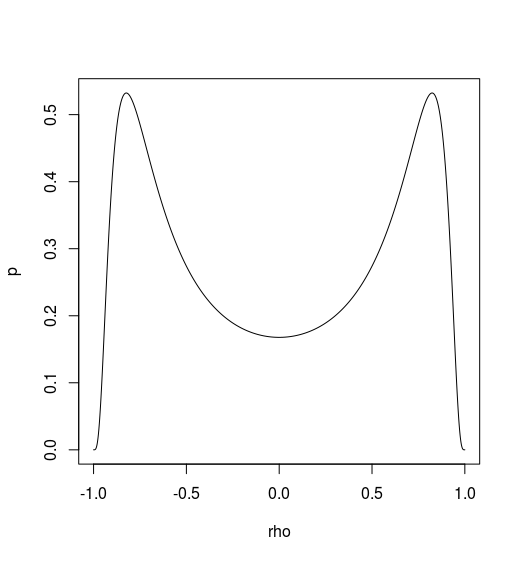
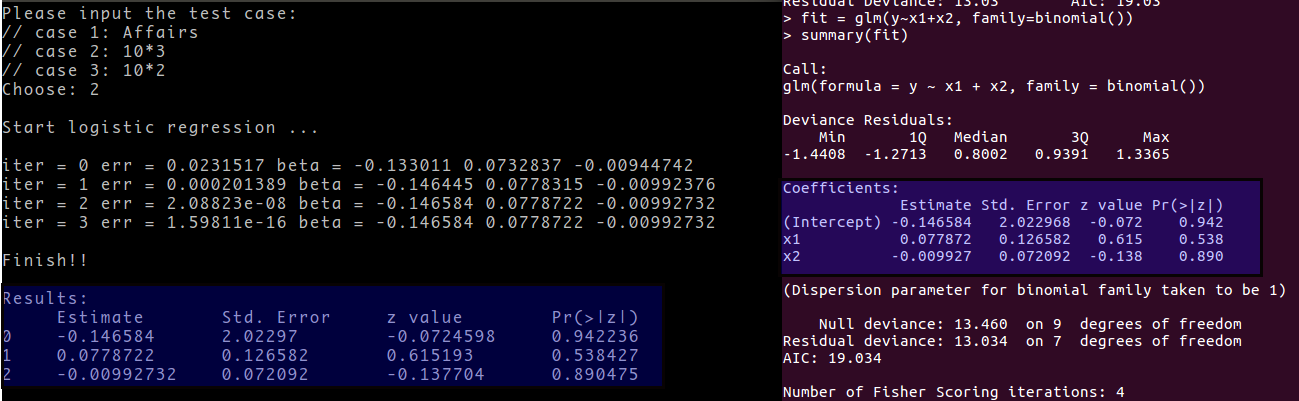
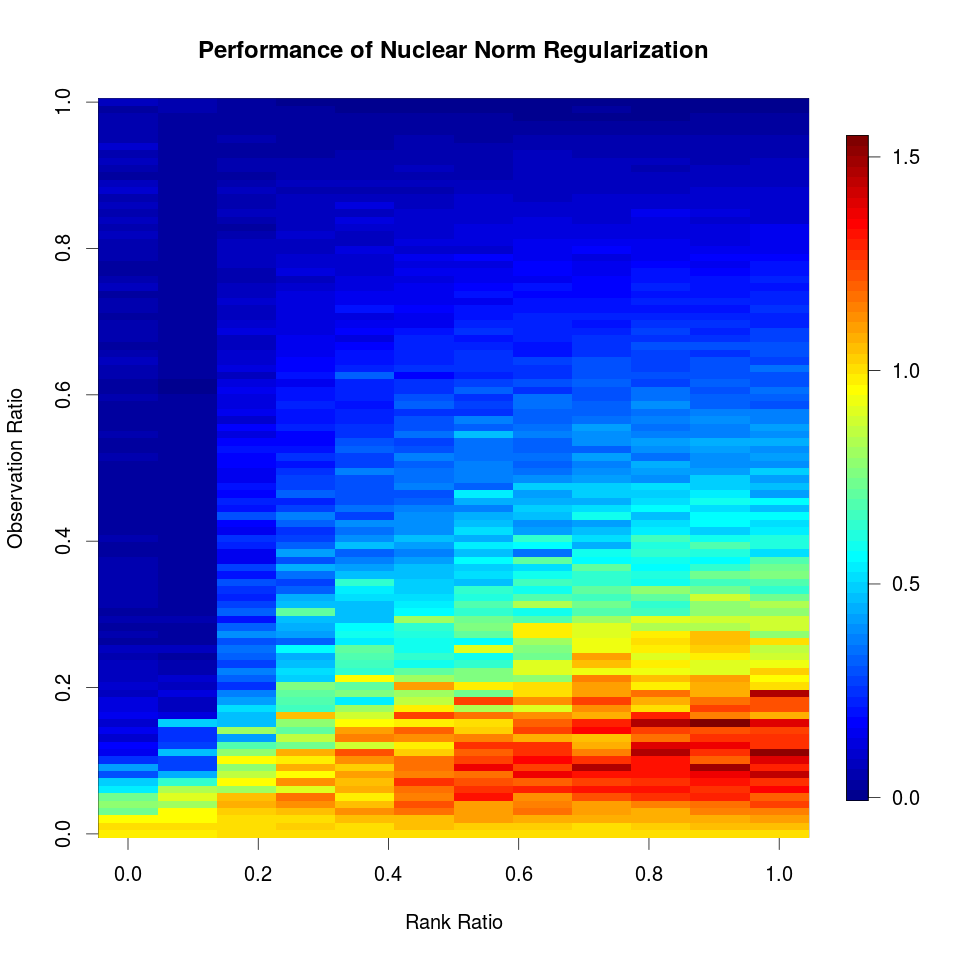
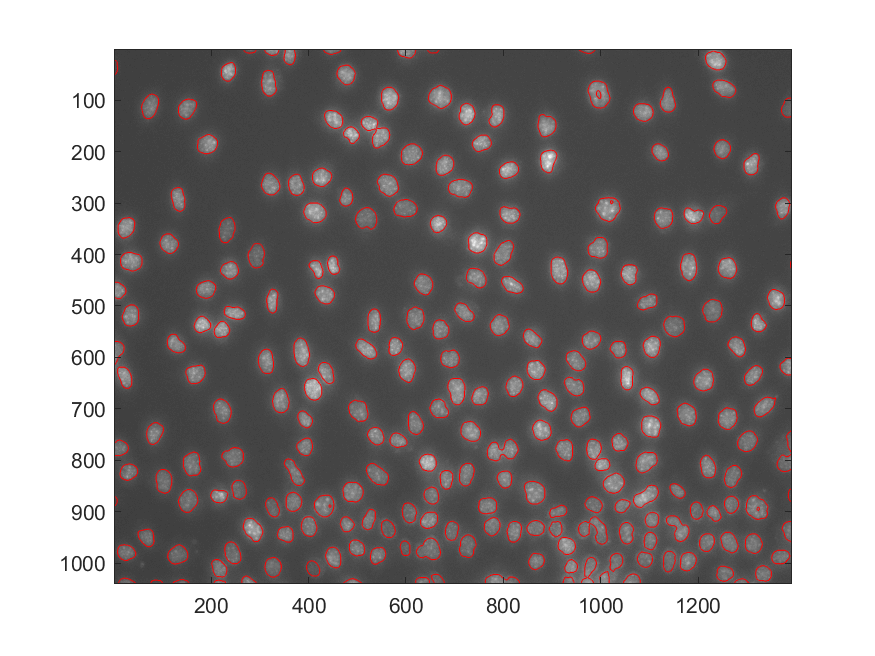
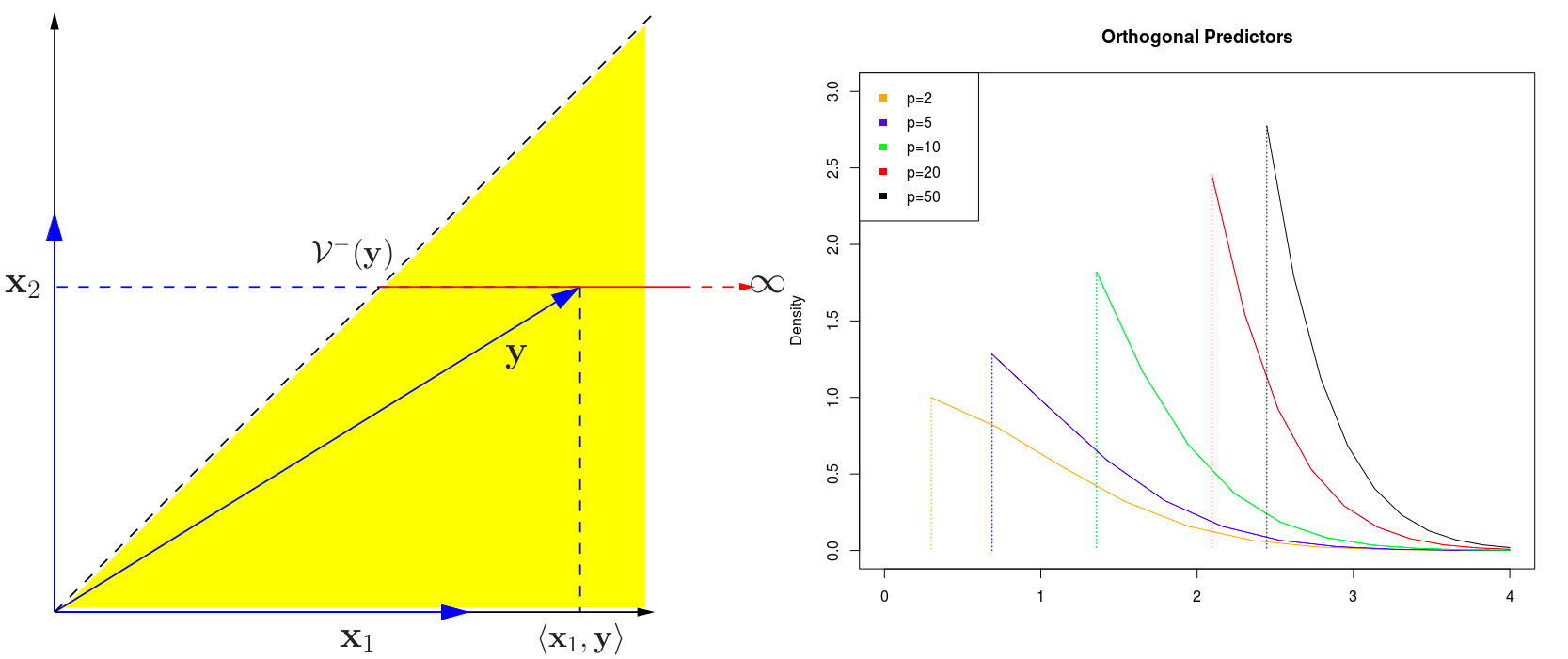
Causal Inference on Distribution Functions
February 20, 2024 (Update: )
Model-X Knockoffs
April 20, 2024 (Update: )
MMRM: Mixed-Models for Repeated Measures
January 10, 2024 (Update: )
This post is based on vignettes of MMRM R package: https://openpharma.github.io/mmrm/main/index.html
sctransform: Normalization using Regularized Negative Binomial Regression
February 24, 2024 (Update: )
Effective Gene Expression Prediction
January 26, 2024 (Update: )
BAMLSS: Flexible Bayesian Additive Joint Model
January 31, 2024 (Update: )
Joint Model in High Dimension
January 31, 2024 (Update: )
FDR Control in GLM
January 15, 2024 (Update: )
One-way Matching with Low Rank
January 06, 2024 (Update: )
This post is for Chen, Shuxiao, Sizun Jiang, Zongming Ma, Garry P. Nolan, and Bokai Zhu. “One-Way Matching of Datasets with Low Rank Signals.” arXiv, October 3, 2022.
FDR Control via Data Splitting
December 19, 2020 (Update: )
This note is for Dai, C., Lin, B., Xing, X., & Liu, J. S. (2020). False Discovery Rate Control via Data Splitting. ArXiv:2002.08542 [Stat].
CountSplit for scRNA Data
December 08, 2023 (Update: )
Lamian: Differential Pseudotime Analysis
September 14, 2023 (Update: )
MM algorithm for Variance Components Models
November 01, 2019 (Update: )
The post is based on Zhou, H., Hu, L., Zhou, J., & Lange, K. (2019). MM Algorithms for Variance Components Models. Journal of Computational and Graphical Statistics, 28(2), 350–361.
fGWAS: Dynamic Model for GWAS
June 11, 2023 (Update: )
Time-varying Group Sparse Additive Model for GWAS
June 11, 2023 (Update: )
Benchmarking Algorithms for Gene Regulatory Network Inference
July 14, 2023 (Update: )
GWAS of Longitudinal Trajectories at Biobank Scale
June 11, 2023 (Update: )
Magnetic Field Orientations in Star Formation
January 12, 2022 (Update: )
LD Score Regression
December 15, 2022 (Update: )
Cox Regression
August 17, 2017 (Update: ) 0 Comments
Survival analysis examines and models the time it takes for events to occur. It focuses on the distribution of survival times. There are many well known methods for estimating unconditional survival distribution, and they examines the relationship between survival and one or more predictors, usually terms covariates in the survival-analysis literature. And Cox Proportional-Hazards regression model is one of the most widely used method of survival analysis.
Similarity Network Fusion
December 28, 2022 (Update: )
This post is for Wang, B., Mezlini, A. M., Demir, F., Fiume, M., Tu, Z., Brudno, M., Haibe-Kains, B., & Goldenberg, A. (2014). Similarity network fusion for aggregating data types on a genomic scale. Nature Methods, 11(3), Article 3. and a related paper Ruan, P., Wang, Y., Shen, R., & Wang, S. (2019). Using association signal annotations to boost similarity network fusion. Bioinformatics, 35(19), 3718–3726.
Rare Variant Association Testing
July 18, 2019 (Update: )
This note is based on
- Wu, M. C., Lee, S., Cai, T., Li, Y., Boehnke, M., & Lin, X. (2011). Rare-Variant Association Testing for Sequencing Data with the Sequence Kernel Association Test. American Journal of Human Genetics, 89(1), 82–93.
- Wang, M. H., Weng, H., Sun, R., Lee, J., Wu, W. K. K., Chong, K. C., & Zee, B. C.-Y. (2017). A Zoom-Focus algorithm (ZFA) to locate the optimal testing region for rare variant association tests. Bioinformatics, 33(15), 2330–2336.
The General Decision Problem
May 06, 2019 (Update: )
This note is based on Chapter 1 of Lehmann EL, Romano JP. Testing statistical hypotheses. Springer Science & Business Media; 2006 Mar 30.
Machine Learning for Multi-omics Data
July 15, 2022 (Update: )
This note is based on Cai, Z., Poulos, R. C., Liu, J., & Zhong, Q. (2022). Machine learning for multi-omics data integration in cancer. IScience, 25(2), 103798.
Differentiable Sorting and Ranking
November 04, 2022 (Update: )
This note is for Blondel, M., Teboul, O., Berthet, Q., & Djolonga, J. (2020). Fast Differentiable Sorting and Ranking (arXiv:2002.08871). arXiv.
Joint Local False Discovery Rate in GWAS
November 12, 2022 (Update: )
Generative Bootstrap/Multi-purpose Samplers
September 22, 2021 (Update: )
This post is based on the first version of Shin, M., Wang, L., & Liu, J. S. (2020). Scalable Uncertainty Quantification via GenerativeBootstrap Sampler., which is lately updated as Shin, M., Wang, S., & Liu, J. S. (2022). Generative Multiple-purpose Sampler for Weighted M-estimation (arXiv:2006.00767; Version 2). arXiv.
High Dimensional Linear Discriminant Analysis
July 15, 2019 (Update: )
Joint Model of Longitudinal and Survival Data
October 02, 2022 (Update: )
This post is based on Rizopoulos, D. (2017). An Introduction to the Joint Modeling of Longitudinal and Survival Data, with Applications in R. 235.
Conformal Inference
September 22, 2021 (Update: ) 0 Comments
The note is based on Lei, J., G’Sell, M., Rinaldo, A., Tibshirani, R. J., & Wasserman, L. (2018). Distribution-Free Predictive Inference for Regression. Journal of the American Statistical Association, 113(523), 1094–1111. and Tibshirani, R. J., Candès, E. J., Barber, R. F., & Ramdas, A. (2019). Conformal Prediction Under Covariate Shift. Proceedings of the 33rd International Conference on Neural Information Processing Systems, 2530–2540.
Multicenter IPF-PRO Registry Cohort
August 25, 2022 (Update: )
Robust Registration of 2D and 3D Point Sets
November 05, 2020 (Update: )
This note is for Fitzgibbon, A. W. (2003). Robust registration of 2D and 3D point sets. Image and Vision Computing, 21(13), 1145–1153.
Test of Monotonicity by Calibrating for Linear Functions
May 11, 2022 (Update: )
Estimation of Location and Scale Parameters of Continuous Density
March 22, 2022 (Update: )
This note is for Pitman, E. J. G. (1939). The Estimation of the Location and Scale Parameters of a Continuous Population of any Given Form. Biometrika, 30(3/4), 391–421. and Kagan, AM & Rukhin, AL. (1967). On the estimation of a scale parameter. Theory of Probability \& Its Applications, 12, 672–678.
Cross-Validation for High-Dimensional Ridge and Lasso
September 16, 2021 (Update: ) 0 Comments
This note collects several references on the research of cross-validation.
Surrogate Splits in Classification and Regression Trees
January 08, 2020 (Update: )
This note is for Section 5.3 of Breiman, L. (Ed.). (1998). Classification and regression trees (1. CRC Press repr). Chapman & Hall/CRC.
A pHMM Algorithm for Correcting Long Reads
May 26, 2021 (Update: ) 0 Comments
Infinite Relational Model
November 18, 2021 (Update: ) 0 Comments
This note is based on Kemp, C., Tenenbaum, J. B., Griffiths, T. L., Yamada, T., & Ueda, N. (n.d.). Learning Systems of Concepts with an Infinite Relational Model. 8. and Saad, F. A., & Mansinghka, V. K. (2021). Hierarchical Infinite Relational Model. ArXiv:2108.07208 [Cs, Stat].
Surprises in High-Dimensional Ridgeless Least Squares Interpolation
June 24, 2019 (Update: )
This post is based on Hastie, T., Montanari, A., Rosset, S., & Tibshirani, R. J. (2019). Surprises in High-Dimensional Ridgeless Least Squares Interpolation. 53.
Local Tracklets Filtering and Global Tracklets Association
July 05, 2021 (Update: ) 0 Comments
Instance Segmentation with Cosine Embeddings
April 25, 2021 (Update: ) 0 Comments
Illustrate Path Sampling by Stan Programming
March 06, 2019 (Update: ) 0 Comments
This post reviewed the topic of path sampling in the lecture slides of STAT 5020, and noted a general path sampling described by Gelman and Meng (1998), then used a toy example to illustrate it with Stan programming language.
Bootstrap Hypothesis Testing
March 03, 2019 (Update: ) 0 Comments
This report is motivated by comments under Larry’s post, Modern Two-Sample Tests.
Monetone B-spline Smoothing
March 09, 2021 (Update: ) 0 Comments
This note is based on He, X., & Shi, P. (1998). Monotone B-Spline Smoothing. Journal of the American Statistical Association, 93(442), 643–650., and the reproduced simulations are based on the updated algorithm, Ng, P., & Maechler, M. (2007). A fast and efficient implementation of qualitatively constrained quantile smoothing splines. Statistical Modelling, 7(4), 315–328.
Principal Curves
September 28, 2020 (Update: )
This post is mainly based on Hastie, T., & Stuetzle, W. (1989). Principal Curves. Journal of the American Statistical Association.
Metabolic Network and Their Evolution
December 31, 2018 (Update: )
Sequence Alignment in EHR
November 12, 2020 (Update: )
Efficient ICP Variants
November 07, 2020 (Update: )
Particle Tracking as Linear Assignment Problem
September 24, 2020 (Update: )
Eleven Challengs in Single Cell Data Science
June 08, 2020 (Update: )
CFPCA for Human Movement Data
April 26, 2020 (Update: )
Jackknife and Mutual Information
January 07, 2019 (Update: ) 0 Comments
In this note, the material about Jackknife is based on Wasserman (2006) and Efron and Hastie (2016), while the Jackknife estimation of Mutual Information is based on Zeng et al. (2018).
Common Functional Principal Components
February 29, 2020 (Update: )
This post is based on Benko, M., Härdle, W., & Kneip, A. (2009). Common functional principal components. The Annals of Statistics, 37(1), 1–34.
Equicorrelation Matrix
February 22, 2020 (Update: )
kjytay’s blog summarizes some properties of equicorrelation matix, which has the following form,
Exponential Twisting in Importance Sampling
September 18, 2019 (Update: )
This note is based on Ma, J., Du, K., & Gu, G. (2019). An efficient exponential twisting importance sampling technique for pricing financial derivatives. Communications in Statistics - Theory and Methods, 48(2), 203–219.
Generalized Matrix Decomposition
January 17, 2020 (Update: )
This post is based on the talk given by Dr. Yue Wang at the Department of Statistics and Data Science, Southern University of Science and Technology on Jan. 04, 2020.
Statistical Inference with Unnormalized Models
February 10, 2020 (Update: )
This post is based on the talk given by T. Kanamori at the 11th ICSA International Conference on Dec. 22nd, 2019.
Tweedie's Formula and Selection Bias
March 11, 2019 (Update: )
Prof. Inchi HU will give a talk on Large Scale Inference for Chi-squared Data tomorrow, which proposes the Tweedie’s formula in the Bayesian hierarchical model for chi-squared data, and he mentioned a thought-provoking paper, Efron, B. (2011). Tweedie’s Formula and Selection Bias. Journal of the American Statistical Association, 106(496), 1602–1614., which is the focus of this note.
Gradient-based Sparse Principal Component Analysis
January 05, 2020 (Update: )
This post is based on the talk, Gradient-based Sparse Principal Component Analysis, given by Dr. Yixuan Qiu at the Department of Statistics and Data Science, Southern University of Science and Technology on Jan. 05, 2020.
Quantitative Genetics
December 21, 2019 (Update: )
This post is based on the Pao-Lu Hsu Award Lecture given by Prof. Hongyu Zhao at the 11th ICSA International Conference on Dec. 21th, 2019.
Registration Problem in Functional Data Analysis
January 21, 2020 (Update: )
This post is based on the seminar, Data Acquisition, Registration and Modelling for Multi-dimensional Functional Data, given by Prof. Shi.
Rademacher Complexity
January 16, 2020 (Update: )
This post is based on the material of the second lecture of STAT 6050 instructed by Prof. Wicker, and mainly refer some more formally description from the book, Mehryar Mohri, Afshin Rostamizadeh, Ameet Talwalkar - Foundations of Machine Learning-The MIT Press (2012).
CEASE
December 20, 2019 (Update: )
This post is based on the Peter Hall Lecture given by Prof. Jianqing Fan at the 11th ICSA International Conference on Dec. 20th, 2019.
Theoretical Results of Lasso
March 26, 2019 (Update: )
Prof. Jon A. WELLNER introduced the application of a new multiplier inequality on lasso in the distinguish lecture, which reminds me that it is necessary to read more theoretical results of lasso, and so this is the post, which is based on Hastie, T., Tibshirani, R., & Wainwright, M. (2015). Statistical Learning with Sparsity. 362.
NGS for NGS
January 11, 2020 (Update: )
This post is based on the talk, Next-Generation Statistical Methods for Association Analysis of Now-Generation Sequencing Studies, given by Dr. Xiang Zhan at the Department of Statistics and Data Science, Southern University of Science and Technology on Jan. 05, 2020.
Group Inference in High Dimensions
December 17, 2019 (Update: )
This post is based on the slides for the talk given by Zijian Guo at The International Statistical Conference In Memory of Professor Sik-Yum Lee
Gibbs Sampler for Finding Motif
December 10, 2018 (Update: )
This post is the online version of my report for the Project 2 of STAT 5050 taught by Prof. Wei.
A Stochastic Model for Evolution of Metabolic Network
August 07, 2018 (Update: )
This post is the notes for Mithani et al. (2009).
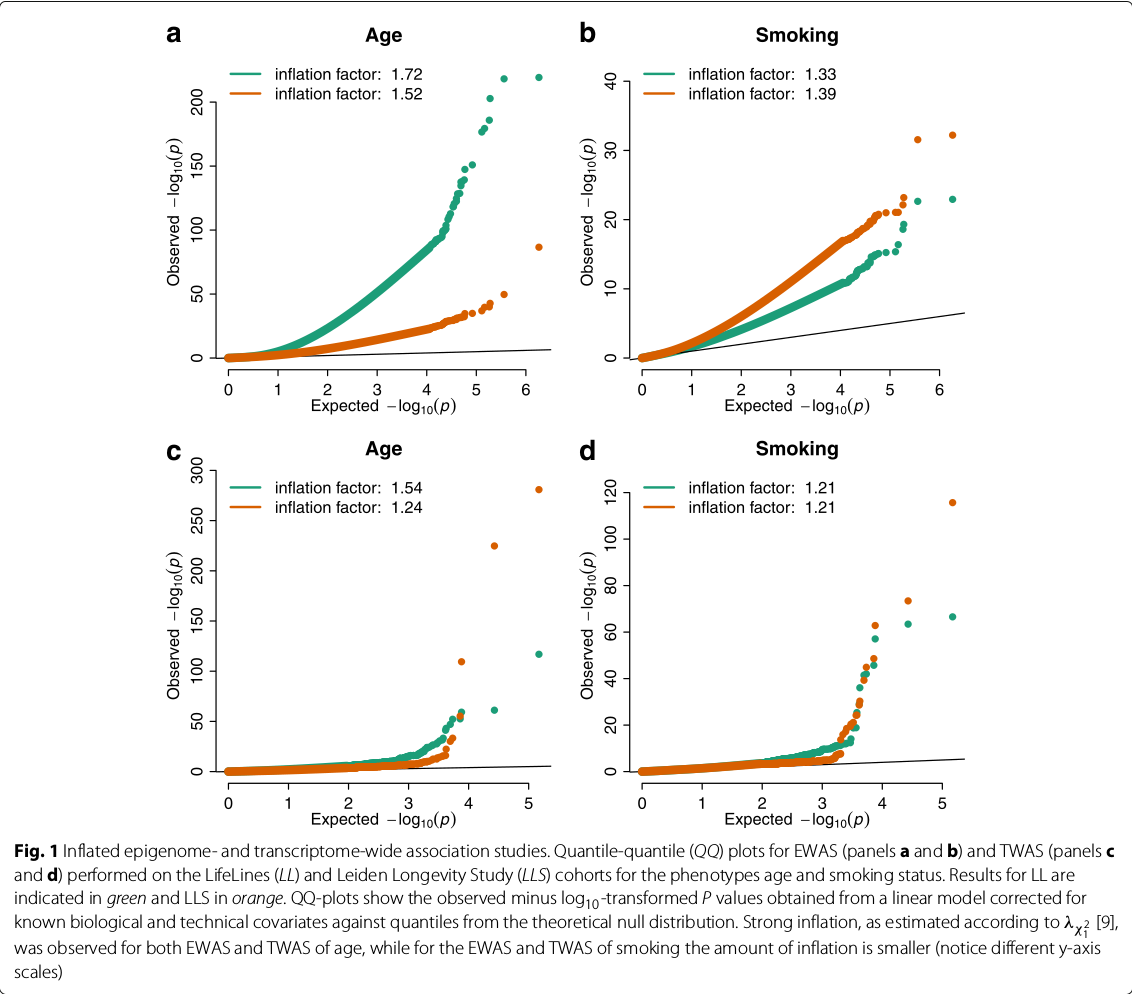
Controlling bias and inflation in EWAS/TWAS
December 04, 2019 (Update: )
Multivariate Mediation Effects
November 04, 2019 (Update: )
This note is based on Huang, Y.-T. (2019). Variance component tests of multivariate mediation effects under composite null hypotheses. Biometrics, 0(0).
Union-intersection tests and Intersection-union tests
December 02, 2019 (Update: )
This post is based on section 8.3 of Casella and Berger (2001).
Generalized Functional Linear Models with Semiparametric Single-index Interactions
October 29, 2019 (Update: )
This post is based on Li, Y., Wang, N., & Carroll, R. J. (2010). Generalized Functional Linear Models With Semiparametric Single-Index Interactions. Journal of the American Statistical Association, 105(490), 621–633.
Gaussian DAGs on Network Data
November 19, 2019 (Update: )
This post is based on Li, H., & Zhou, Q. (2019). Gaussian DAGs on network data. ArXiv:1905.10848 [Cs, Stat].
Optimal estimation of functionals of high-dimensional mean and covariance matrix
August 26, 2019 (Update: )
This post is based on Fan, J., Weng, H., & Zhou, Y. (2019). Optimal estimation of functionals of high-dimensional mean and covariance matrix. ArXiv:1908.07460 [Math, Stat].
SIR and Its Implementation
January 05, 2019 (Update: ) 0 Comments
Link-free v.s. Semiparametric
January 08, 2019 (Update: )
This note is based on Li (1991) and Ma and Zhu (2012).
Sparse LDA
September 17, 2019 (Update: )
This note is based on Shao, J., Wang, Y., Deng, X., & Wang, S. (2011). Sparse linear discriminant analysis by thresholding for high dimensional data. The Annals of Statistics, 39(2), 1241–1265.
Feature Annealed Independent Rules
September 17, 2019 (Update: ) 0 Comments
This note is based on Fan, J., & Fan, Y. (2008). High-dimensional classification using features annealed independence rules. The Annals of Statistics, 36(6), 2605–2637.
Dantzig Selector
August 16, 2019 (Update: )
This post is based on Candes, E., & Tao, T. (2007). The Dantzig selector: Statistical estimation when $p$ is much larger than $n$. The Annals of Statistics, 35(6), 2313–2351.
MLE for MTP2
July 05, 2019 (Update: )
This post is based on Lauritzen, S., Uhler, C., & Zwiernik, P. (2019). Maximum likelihood estimation in Gaussian models under total positivity. The Annals of Statistics, 47(4), 1835–1863.
TreeClone
July 08, 2019 (Update: )
Minimax Lower Bounds
June 28, 2019 (Update: )
This note is based on Chapter 15 of Wainwright, M. (2019). High-Dimensional Statistics: A Non-Asymptotic Viewpoint (Cambridge Series in Statistical and Probabilistic Mathematics). Cambridge: Cambridge University Press.
Change Points
May 28, 2019 (Update: )
Fourier Series
May 07, 2019 (Update: )
M-estimator
May 09, 2019 (Update: )
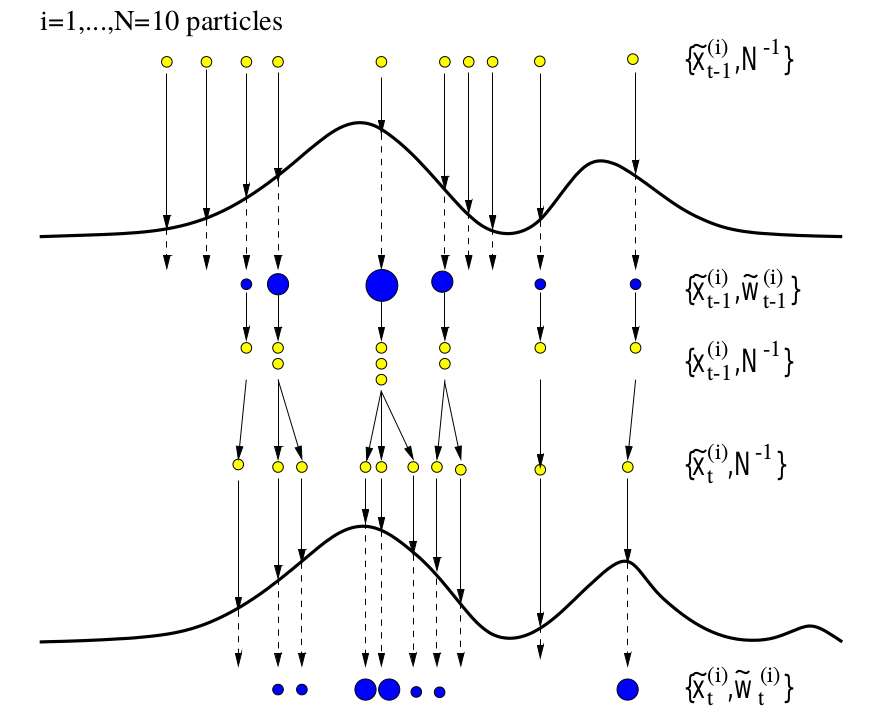
Particle Filtering and Smoothing
January 18, 2019 (Update: ) 0 Comments
This note is for Doucet, A., & Johansen, A. M. (2009). A tutorial on particle filtering and smoothing: Fifteen years later. Handbook of Nonlinear Filtering, 12(656–704), 3. For the sake of clarity, I split the general SMC methods (section 3) into my next post.
Generalized Gradient Descent
March 20, 2019 (Update: )
I read the topic in kiytay’s blog: Proximal operators and generalized gradient descent, and then read its reference, Hastie et al. (2015), and write some program to get a better understanding.
Multiple Object Tracking
March 26, 2019 (Update: )
This note is for Luo, W., Xing, J., Milan, A., Zhang, X., Liu, W., Zhao, X., & Kim, T.-K. (2014). Multiple Object Tracking: A Literature Review. ArXiv:1409.7618 [Cs].
The Gibbs Sampler
June 04, 2017 (Update: ) 0 Comments
Gibbs sampler is an iterative algorithm that constructs a dependent sequence of parameter values whose distribution converges to the target joint posterior distribution.
Tensor Completion
March 07, 2019 (Update: )
Prof. YUAN Ming will give a distinguish lecture on Low Rank Tensor Methods in High Dimensional Data Analysis. To get familiar with his work on tensor, I read his paper, Yuan, M., & Zhang, C.-H. (2016). On Tensor Completion via Nuclear Norm Minimization. Foundations of Computational Mathematics, 16(4), 1031–1068., which is the topic of this post.
SMC for Protein Folding Problem
February 23, 2019 (Update: )
This note is based on Wong, S. W. K., Liu, J. S., & Kou, S. C. (2018). Exploring the conformational space for protein folding with sequential Monte Carlo. The Annals of Applied Statistics, 12(3), 1628–1654.
Select Prior by Formal Rules
March 04, 2019 (Update: )
Larry wrote that “Noninformative priors are a lost cause” in his post, LOST CAUSES IN STATISTICS II: Noninformative Priors, and he mentioned his review paper Kass and Wasserman (1996) on noninformative priors. This note is for this paper.
Bio-chemical Reaction Networks
February 25, 2019 (Update: )
This note is based on Loskot, P., Atitey, K., & Mihaylova, L. (2019). Comprehensive review of models and methods for inferences in bio-chemical reaction networks.
An Illustration of Importance Sampling
July 16, 2017 (Update: ) 0 Comments
This report shows how to use importance sampling to estimate the expectation.
Sequential Monte Carlo Methods
June 10, 2017 (Update: ) 0 Comments
The first peep to SMC as an abecedarian, a more comprehensive note can be found here.
Chain-Structured Models
September 08, 2017 (Update: ) 0 Comments
There is an important probability distribution used in many applications, the chain-structured model.
The Applications of Monte Carlo
September 07, 2017 (Update: ) 0 Comments
Growing A Polymer
July 17, 2017 (Update: ) 0 Comments
This report implements the simulation of growing a polymer under the self-avoid walk model, and summary the sequential importance sampling techniques for this problem.
Genetic network inference
March 14, 2017 0 Comments
There are my notes when I read the paper called Genetic network inference.
Systems Genetic Approach
March 16, 2017 0 Comments
There are my notes when I read the paper called System Genetic Approach.
MICA
March 17, 2017 0 Comments
There are my notes when I read the paper called Maximal information component analysis.
MINE
March 17, 2017 0 Comments
There are my notes when I read the paper called Detecting Novel Associations in Large Data Sets.
Implement of MINE
March 17, 2017 0 Comments
This is the implement in R of MINE.
Ensemble Learning
May 17, 2017 0 Comments
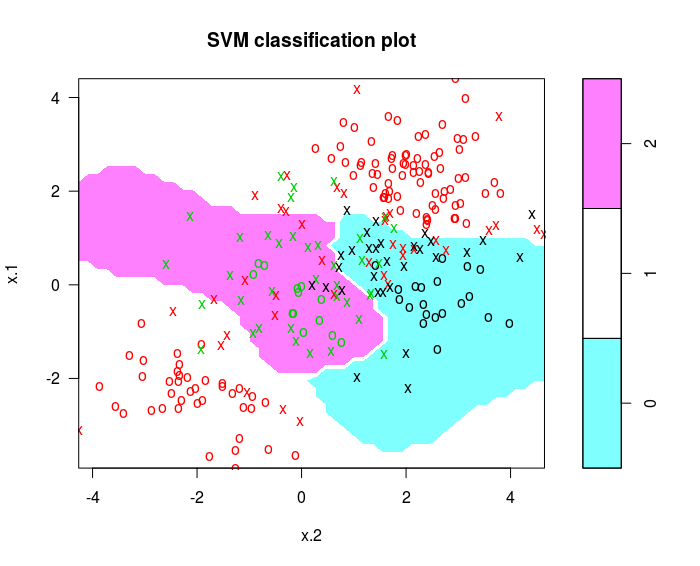
Illustrations of Support Vector Machines
May 18, 2017 0 Comments
Use the e1071 library in R to demonstrate the support vector classifier and the SVM.
One Parameter Models
June 04, 2017 0 Comments
The Normal Model
June 05, 2017 0 Comments
Sequential Monte Carlo samplers
June 11, 2017 0 Comments
SMC for Mixture Distribution
June 11, 2017
ARIMA
July 11, 2017 0 Comments
Any time series without a constant mean over time is nonstationary.
Adaptive Importance Sampling
July 16, 2017 0 Comments
Model Specification
July 17, 2017 0 Comments
For a given time series, how to choose appropriate values for $p, d, q$
A Bayesian Missing Data Problem
July 18, 2017 0 Comments
Metropolis Algorithm
July 21, 2017 0 Comments
Monte Carlo plays a key role in evaluating integrals and simulating stochastic systems, and the most critical step of Monte Carlo algorithm is sampling from an appropriate probability distribution $\pi (\mathbf x)$. There are two ways to solve this problem, one is to do importance sampling, another is to produce statistically dependent samples based on the idea of Markov chain Monte Carlo sampling.
SMC in Biological Problems
July 22, 2017 0 Comments
Estimate Parameters in Logistic Regression
July 30, 2017 0 Comments
Poisson Regression
July 31, 2017 0 Comments
Story about P value
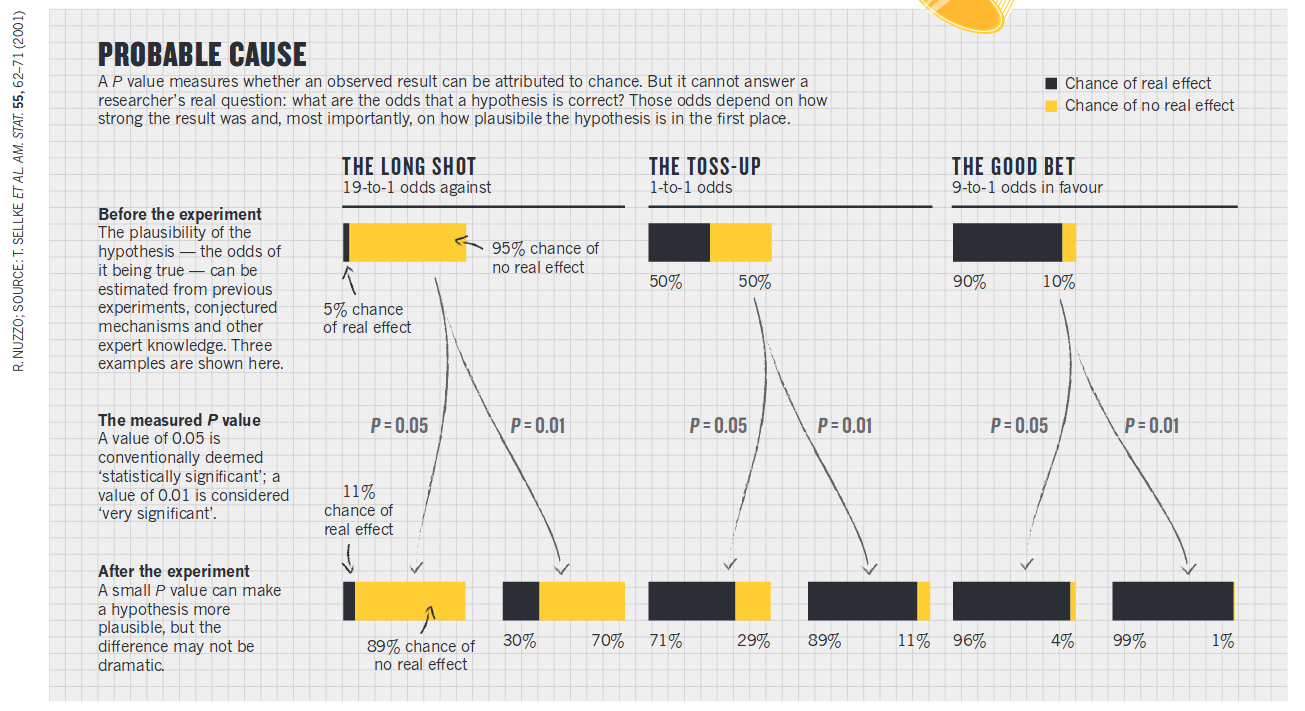
August 09, 2017 0 Comments
“The p value was never meant to be used the way it’s used today.” –Goodman
Conjugate Gradient for Regression
August 13, 2017 0 Comments
The conjugate gradient method is an iterative method for solving a linear system of equations, so we can use conjugate method to estimate the parameters in (linear/ridge) regression.
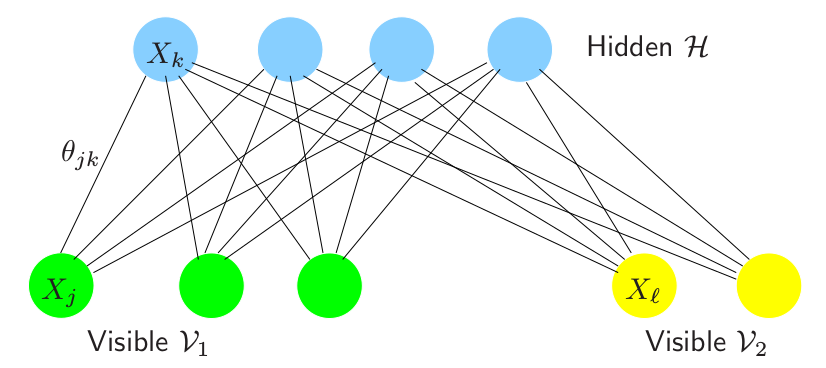
Restricted Boltzmann Machines
August 26, 2017 0 Comments
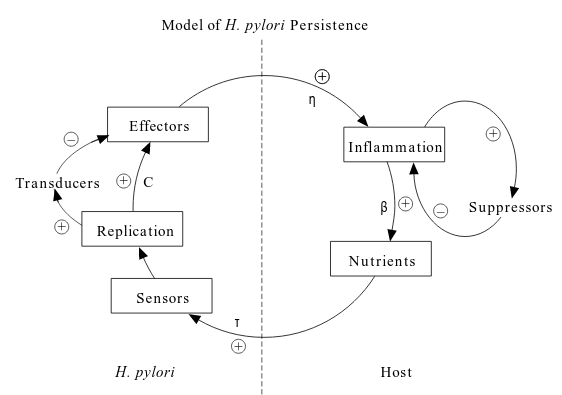
Dynamics of Helicobacter pylori colonization
August 31, 2017 0 Comments
This post is the notes of this paper.
Healthy Human Microbiome
September 01, 2017 0 Comments
Dynamics of Helicobacter pylori Infection
September 01, 2017 0 Comments
Basic Principles of Monte Carlo
September 07, 2017 0 Comments
Persistence of species in the face of environmental stochasticity
September 18, 2017 0 Comments
Sebastian Schreiber gave a talk titled Persistence of species in the face of environmental stochasticity.
A Faster Algorithm for Repeated Linear Regression
September 21, 2017 0 Comments
Repeated Linear Regression means that repeat the fitting of linear regression for many times, and there are some common parts among these regressions.
An R Package: Fit Repeated Linear Regressions
September 26, 2017 0 Comments
Repeated Linear Regressions refer to a set of linear regressions in which there are several same variables.
Stochastic Epidemic Models
October 11, 2017 0 Comments
Discuss three different methods for formulating stochastic epidemic models.
Essentials of Survival Time Analysis
October 11, 2017 0 Comments
This post aims to clarify the relationship between rates and probabilities.
Model-Free Scoring System for Risk Prediction
October 17, 2017 0 Comments
Power Analysis
December 27, 2017 0 Comments
ECOC
August 18, 2018
Gibbs in genetics
August 24, 2018
The note is for Gilks, W. R., Richardson, S., & Spiegelhalter, D. (Eds.). (1995). Markov chain Monte Carlo in practice. CRC press..
Evolutionary Systems Biology
December 30, 2018
The note is for Chapter 1 of Soyer, Orkun S., ed. 2012 Evolutionary Systems Biology. Advances in Experimental Medicine and Biology, 751. New York: Springer.
Small World inside Large Metabolic Networks
January 02, 2019
Counting Process Based Dimension Reduction Methods for Censored Data
January 06, 2019
Reconstruct Gaussian DAG
January 09, 2019
This note is based on Yuan, Y., Shen, X., Pan, W., & Wang, Z. (2019). Constrained likelihood for reconstructing a directed acyclic Gaussian graph. Biometrika, 106(1), 109–125.
Reversible jump Markov chain Monte Carlo
January 10, 2019
The note is for Green, P.J. (1995). “Reversible Jump Markov Chain Monte Carlo Computation and Bayesian Model Determination”. Biometrika. 82 (4): 711–732.
Approximate $\ell_0$-penalized piecewise-constant estimate of graphs
January 13, 2019
PLS in High-Dimensional Regression
January 15, 2019
This note is based on Cook, R. D., & Forzani, L. (2019). Partial least squares prediction in high-dimensional regression. The Annals of Statistics, 47(2), 884–908.
Sequential Monte Carlo Methods
January 19, 2019
This note is for Section 3 of Doucet, A., & Johansen, A. M. (2009). A tutorial on particle filtering and smoothing: Fifteen years later. Handbook of Nonlinear Filtering, 12(656–704), 3., and it is the complement of my previous post.
The Kalman Filter and Extended Kalman Filter
January 21, 2019
Annealed SMC for Bayesian Phylogenetics
January 24, 2019
This note is for Wang, L., Wang, S., & Bouchard-Côté, A. (2018). An Annealed Sequential Monte Carlo Method for Bayesian Phylogenetics. ArXiv:1806.08813 [q-Bio, Stat].
Annealed Importance Sampling
January 28, 2019
This is the note for Neal, R. M. (1998). Annealed Importance Sampling. ArXiv:Physics/9803008.
Calculating Marginal likelihood
January 30, 2019
The First Glimpse into Pseudolikelihood
February 12, 2019
This post caught a glimpse of the pseudolikelihood.
Comparisons of Three Likelihood Criteria
February 12, 2019
Identification of PE Genes in Cell Cycle
February 13, 2019
This note is based on Fan, X., Pyne, S., & Liu, J. S. (2010). Bayesian meta-analysis for identifying periodically expressed genes in fission yeast cell cycle. The Annals of Applied Statistics, 4(2), 988–1013.
Gibbs Sampling for the Multivariate Normal
February 13, 2019
This note is based on Chapter 7 of Hoff PD. A first course in Bayesian statistical methods. Springer Science & Business Media; 2009 Jun 2.
Review of Composite Likelihood
February 13, 2019
This note is based on Varin, C., Reid, N., & Firth, D. (2011). AN OVERVIEW OF COMPOSITE LIKELIHOOD METHODS. Statistica Sinica, 21(1), 5–42., a survey of recent developments in the theory and application of composite likelihood.
Studentized U-statistics
February 15, 2019 0 Comments
In Prof. Shao’s wonderful talk, Wandering around the Asymptotic Theory, he mentioned the Studentized U-statistics. I am interested in the derivation of the variances in the denominator.
Deep Learning
February 16, 2019
This note is based on LeCun, Y., Bengio, Y., & Hinton, G. (2015). Deep learning. Nature, 521(7553), 436–444.
A Bayesian Perspective of Deep Learning
February 17, 2019
This note is for Polson, N. G., & Sokolov, V. (2017). Deep Learning: A Bayesian Perspective. Bayesian Analysis, 12(4), 1275–1304.
Presistency
February 18, 2019
The paper, Greenshtein and Ritov (2004), is recommended by Larry Wasserman in his post Consistency, Sparsistency and Presistency.
Restricted Isometry Property
February 19, 2019
I encounter the term RIP in Larry Wasserman’s post, RIP RIP (Restricted Isometry Property, Rest In Peace), and also find some material in Hastie et al.’s book: Statistical Learning with Sparsity about RIP.
Continuous Time Markov Chain
February 20, 2019
This note is based on Karl Sigman’s IEOR 6711: Continuous-Time Markov Chains.
Stein's Paradox
February 21, 2019
I learned Stein’s Paradox from Larry Wasserman’s post, STEIN’S PARADOX, perhaps I had encountered this term before but I cannot recall anything about it. (I am guilty)
Evaluate Variational Inference
March 07, 2019
A brief summary of the post, Eid ma clack shaw zupoven del ba.
Bernstein Bounds
March 08, 2019
I noticed that the papers of matrix/tensor completion always talk about the Bernstein inequality, then I picked the Bernstein Bounds discussed in Wainwright (2019).
The Correlated Topic Model
March 12, 2019
This note is for Blei, D. M., & Lafferty, J. D. (2007). A correlated topic model of Science. The Annals of Applied Statistics, 1(1), 17–35.
Distributed inference for quantile regression processes
March 13, 2019
This note is for Volgushev, S., Chao, S.-K., & Cheng, G. (2019). Distributed inference for quantile regression processes. The Annals of Statistics, 47(3), 1634–1662.
Functional Data Analysis
March 14, 2019
Functional Data Analysis by Matrix Completion
March 15, 2019
High Dimensional Covariance Matrix Estimation
March 19, 2019
Convergence rates of least squares
March 25, 2019
This note is for Han, Q., & Wellner, J. A. (2017). Convergence rates of least squares regression estimators with heavy-tailed errors.
Joint Summarized by Marginal or Conditional?
March 25, 2019
I happened to read Yixuan’s blog about a question related to the course Statistical Inference, whether two marginal distributions can determine the joint distribution. The question is adopted from Exercise 4.47 of Casella and Berger (2002).
FARM-Test
March 29, 2019
Frequentist Accuracy of Bayesian Estimates
March 31, 2019
This note is for Efron’s slide: Frequentist Accuracy of Bayesian Estimates, which is recommended by Larry’s post: Shaking the Bayesian Machine.
Soft Imputation in Matrix Completion
April 01, 2019
This post is based on Chapter 7 of Statistical Learning with Sparsity: The Lasso and Generalizations, and I wrote R program to reproduce the simulations to get a better understanding.
Coupled Minimum-Cost Flow Cell Tracking
April 02, 2019
Wierd Things in Mixture Models
April 04, 2019
This note is based on Larry’s post, Mixture Models: The Twilight Zone of Statistics.
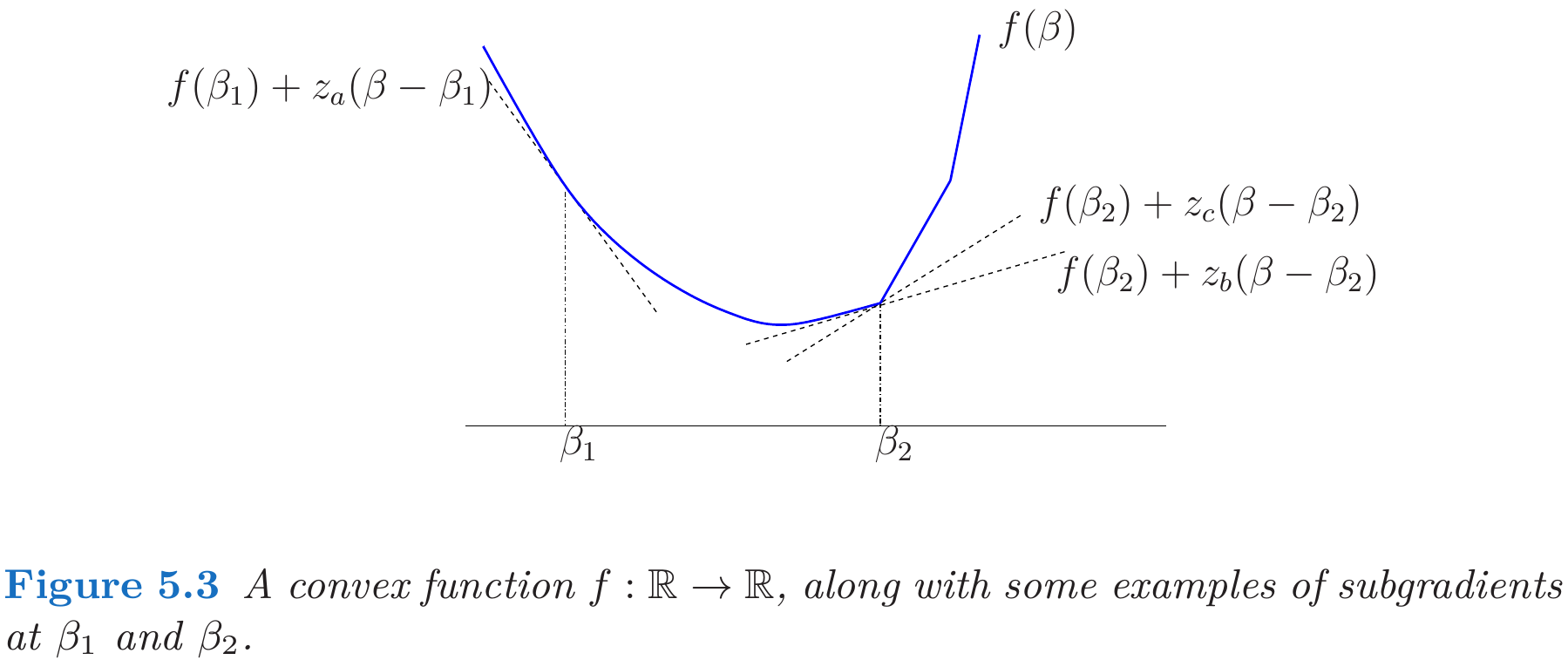
Subgradient
April 08, 2019
This post is mainly based on Hastie et al. (2015), and incorporated with some materials from Watson (1992).
Tracking Multiple Interacting Targets via MCMC-MRF
April 09, 2019
Methods for Cell Tracking
April 09, 2019
This post is for the survey paper, Meijering, E., Dzyubachyk, O., & Smal, I. (2012). Chapter nine - Methods for Cell and Particle Tracking. In P. M. conn (Ed.), Methods in Enzymology (pp. 183–200).
Normalizing Constant
April 10, 2019
Larry discussed the normalizing constant paradox in his blog.
Multiple Tracking with Rao-Blackwellized marginal particle filtering
April 10, 2019
Statistical Inference for Lasso
April 15, 2019
This note is based on the Chapter 6 of Hastie, T., Tibshirani, R., & Wainwright, M. (2015). Statistical Learning with Sparsity. 362..
Least Squares for SIMs
April 15, 2019
In the last lecture of STAT 5030, Prof. Lin shared one of the results in the paper, Neykov, M., Liu, J. S., & Cai, T. (2016). L1-Regularized Least Squares for Support Recovery of High Dimensional Single Index Models with Gaussian Designs. Journal of Machine Learning Research, 17(87), 1–37., or say the start point for the paper—the following Lemma. Because it seems that the condition and the conclusion is completely same with Sliced Inverse Regression, except for a direct interpretation—the least square regression.
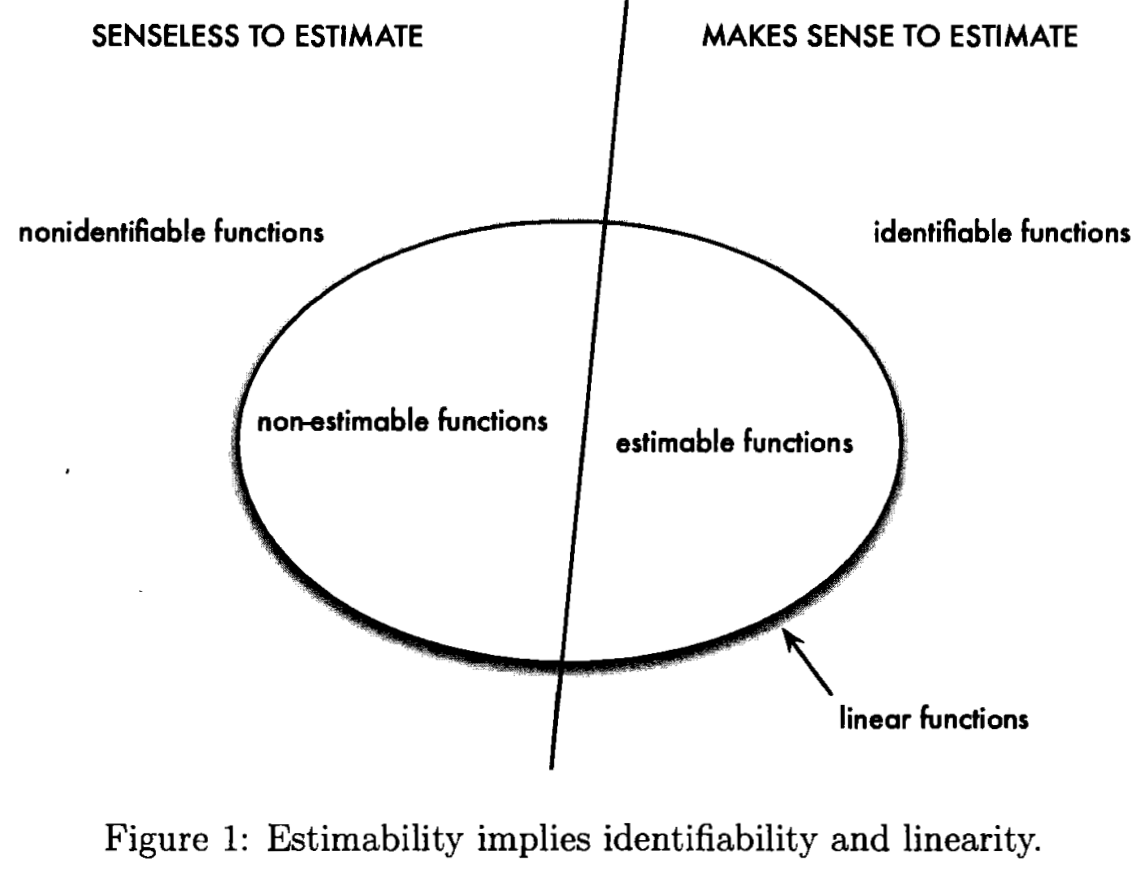
Identifiability and Estimability
April 20, 2019
Materials from STAT 5030.
Self-normalized Limit Theory and Stein's Method
May 01, 2019
This note consists of the lecture material of STAT 6060 taught by Prof. Shao, four homework (indexed by “Homework”) and several personal comments (indexed by “Note”).
Medicine Meets AI
June 23, 2019
Last two days, I attended the conference Medicine Meets AI 2019: East Meets West, which help me know more AI from the industrial and medical perspective.
Bayesian Conjugate Gradient Method
June 27, 2019
This note is for Cockayne, J., Oates, C. J., Ipsen, I. C. F., & Girolami, M. (2018). A Bayesian Conjugate Gradient Method. Bayesian Analysis.
Global data association for MOT using network flows
July 10, 2019
This note is based on Li Zhang, Yuan Li, & Nevatia, R. (2008). Global data association for multi-object tracking using network flows. 2008 IEEE Conference on Computer Vision and Pattern Recognition, 1–8.
Canonical Variate Analysis
July 16, 2019
This note is based on Campbell, N. A. (1979). CANONICAL VARIATE ANALYSIS: SOME PRACTICAL ASPECTS. 243.
SMC-PHD Filter
July 17, 2019
This post is based on Ristic, B., Clark, D., & Vo, B. (2010). Improved SMC implementation of the PHD filter. 2010 13th International Conference on Information Fusion, 1–8.
Multi-estimate extraction for SMC-PHD
July 17, 2019
This post is based on Li, T., Corchado, J. M., Sun, S., & Fan, H. (2017). Multi-EAP: Extended EAP for multi-estimate extraction for SMC-PHD filter. Chinese Journal of Aeronautics, 30(1), 368–379.
A Optimal Control Approach for Deep Learning
July 19, 2019
This note is based on Li, Q., & Hao, S. (2018). An Optimal Control Approach to Deep Learning and Applications to Discrete-Weight Neural Networks. ArXiv:1803.01299 [Cs].
High-dimensional linear mixed-effect model
July 21, 2019
This post is based on Li, S., Cai, T. T., & Li, H. (2019). Inference for high-dimensional linear mixed-effects models: A quasi-likelihood approach. ArXiv:1907.06116 [Stat].
An Adaptive Algorithm for online FDR
July 21, 2019
This post is based on Ramdas, A., Zrnic, T., Wainwright, M., & Jordan, M. (2018). SAFFRON: An adaptive algorithm for online control of the false discovery rate. ArXiv:1802.09098 [Cs, Math, Stat].
The Simplex Method
July 23, 2019
This note is based on Chapter 13 of Nocedal, J., & Wright, S. (2006). Numerical optimization. Springer Science & Business Media.
Reluctant Interaction Modeling
July 23, 2019
This note is based on Yu, G., Bien, J., & Tibshirani, R. (2019). Reluctant Interaction Modeling. ArXiv:1907.08414 [Stat].
Additive Bayesian Variable Selection
August 05, 2019
This post is based on Rossell, D., & Rubio, F. J. (2019). Additive Bayesian variable selection under censoring and misspecification. ArXiv:1907.13563 [Math, Stat].
Interior-point Method
August 16, 2019
Nocedal and Wright (2006) and Boyd and Vandenberghe (2004) present slightly different introduction on Interior-point method. More specifically, the former one only considers equality constraints, while the latter incorporates the inequality constraints.
Debiased Lasso
September 08, 2019
This post is based on Section 6.4 of Hastie, Trevor, Robert Tibshirani, and Martin Wainwright. “Statistical Learning with Sparsity,” 2016, 362.
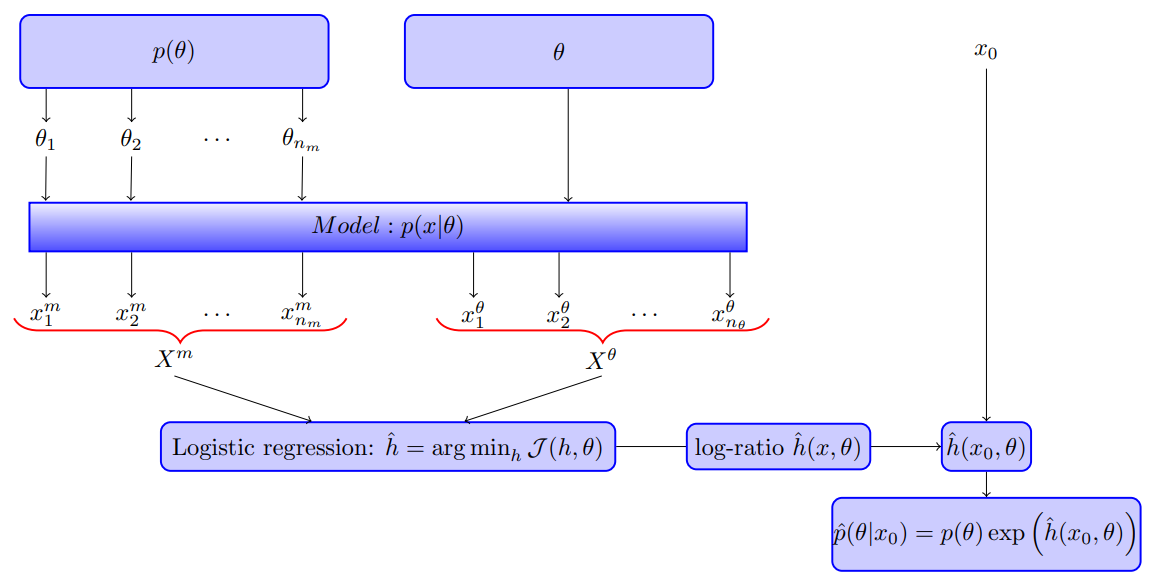
Likelihood-free inference by ratio estimation
September 09, 2019 0 Comments
This note is for Thomas, O., Dutta, R., Corander, J., Kaski, S., & Gutmann, M. U. (2016). Likelihood-free inference by ratio estimation. ArXiv:1611.10242 [Stat]., and I got this paper from Xi’an’s blog.
Basic of $B$-splines
September 09, 2019 0 Comments
This note is based on de Boor, C. (1978). A Practical Guide to Splines, Springer, New York.
Functional PCA
September 20, 2019
This post is based on Ramsay, J. O., & Silverman, B. W. (2005). Functional data analysis (Second edition). New York, NY: Springer.
Multiple human tracking with RGB-D data
September 20, 2019
This note is based on the survey paper Camplani, M., Paiement, A., Mirmehdi, M., Damen, D., Hannuna, S., Burghardt, T., & Tao, L. (2016). Multiple human tracking in RGB-depth data: A survey. IET Computer Vision, 11(4), 265–285.
ABC for Socks
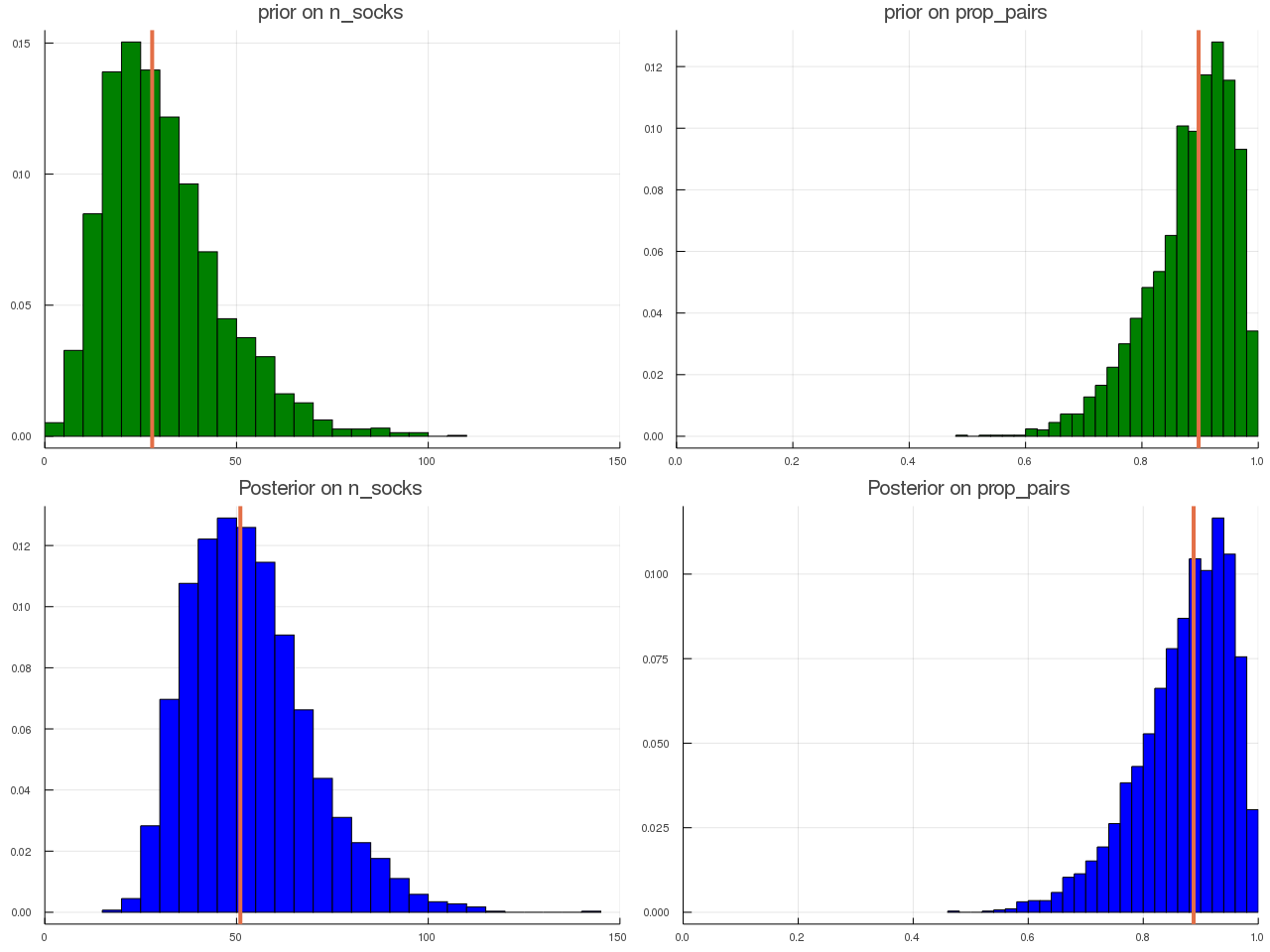
September 24, 2019 0 Comments
This post is based on Prof. Robert’s slides on JSM 2019 and an intuitive blog from Rasmus Bååth.
Optimality for Sparse Group Lasso
September 29, 2019
This note is based on Cai, T. T., Zhang, A., & Zhou, Y. (2019). Sparse Group Lasso: Optimal Sample Complexity, Convergence Rate, and Statistical Inference. ArXiv:1909.09851 [Cs, Math, Stat].
Kernel Ridgeless Regression Can Generalize
September 30, 2019
This note is based on Liang, T., & Rakhlin, A. (2018). Just Interpolate: Kernel “Ridgeless” Regression Can Generalize. ArXiv:1808.00387 [Cs, Math, Stat].
Sub Gaussian
October 05, 2019
This post is based on Wainwright (2019).
Linear Regression with Partially Shuffled Data
October 08, 2019
This post is based on Slawski, M., Diao, G., & Ben-David, E. (2019). A Pseudo-Likelihood Approach to Linear Regression with Partially Shuffled Data. ArXiv:1910.01623 [Cs, Stat].
Noise Outsourcing
October 10, 2019
I learnt the term Noise Outsourcing in kjytay’s blog, which is based on Teh Yee Whye’s IMS Medallion Lecture at JSM 2019.
Isotropic vs. Anisotropic
October 24, 2019
I came across isotropic and anisotropic covariance functions in kjytay’s blog, and then I found more materials, chapter 4 from the book Gaussian Processes for Machine Learning, via the reference in StackExchange: What is an isotropic (spherical) covariance matrix?.
Partial Least Squares for Functional Data
October 31, 2019
This post is based on Delaigle, A., & Hall, P. (2012). Methodology and theory for partial least squares applied to functional data. The Annals of Statistics, 40(1), 322–352.
Model-based Approach for Joint Analysis of Single-cell data
October 31, 2019
Genetic Relatedness in High-Dimensional Linear Models
October 31, 2019
This post is based on Guo, Z., Wang, W., Cai, T. T., & Li, H. (2019). Optimal Estimation of Genetic Relatedness in High-Dimensional Linear Models. Journal of the American Statistical Association, 114(525), 358–369.
The Cost of Privacy
November 01, 2019
This note is based on Cai, T. T., Wang, Y., & Zhang, L. (2019). The Cost of Privacy: Optimal Rates of Convergence for Parameter Estimation with Differential Privacy. ArXiv:1902.04495 [Cs, Stat].
Active Contours
November 12, 2019
This post is based on Ray, N., & Acton, S. T. (2002). Active contours for cell tracking. Proceedings Fifth IEEE Southwest Symposium on Image Analysis and Interpretation, 274–278.
Combining $p$-values in Meta Analysis
December 04, 2019
I came across the term meta-analysis in the previous post, and I had another question about nominal size while reading the paper of the previous post, which reminds me Keith’s notes. By coincidence, I also find the topic about meta-analysis in the same notes. Hence, this post is mainly based on Keith’s notes, and reproduce the power curves by myself.
Fantastic Generalization Measures and Where to Find Them
December 06, 2019
The post is based on Jiang, Y., Neyshabur, B., Mobahi, H., Krishnan, D., & Bengio, S. (2019). Fantastic Generalization Measures and Where to Find Them. ArXiv:1912.02178 [Cs, Stat].which was shared by one of my friend in the WeChat Moment, and then I took a quick look.
Quantile Regression Forests
December 10, 2019
This post is based on Meinshausen, N. (2006). Quantile Regression Forests. 17. since a coming seminar is related to such topic.
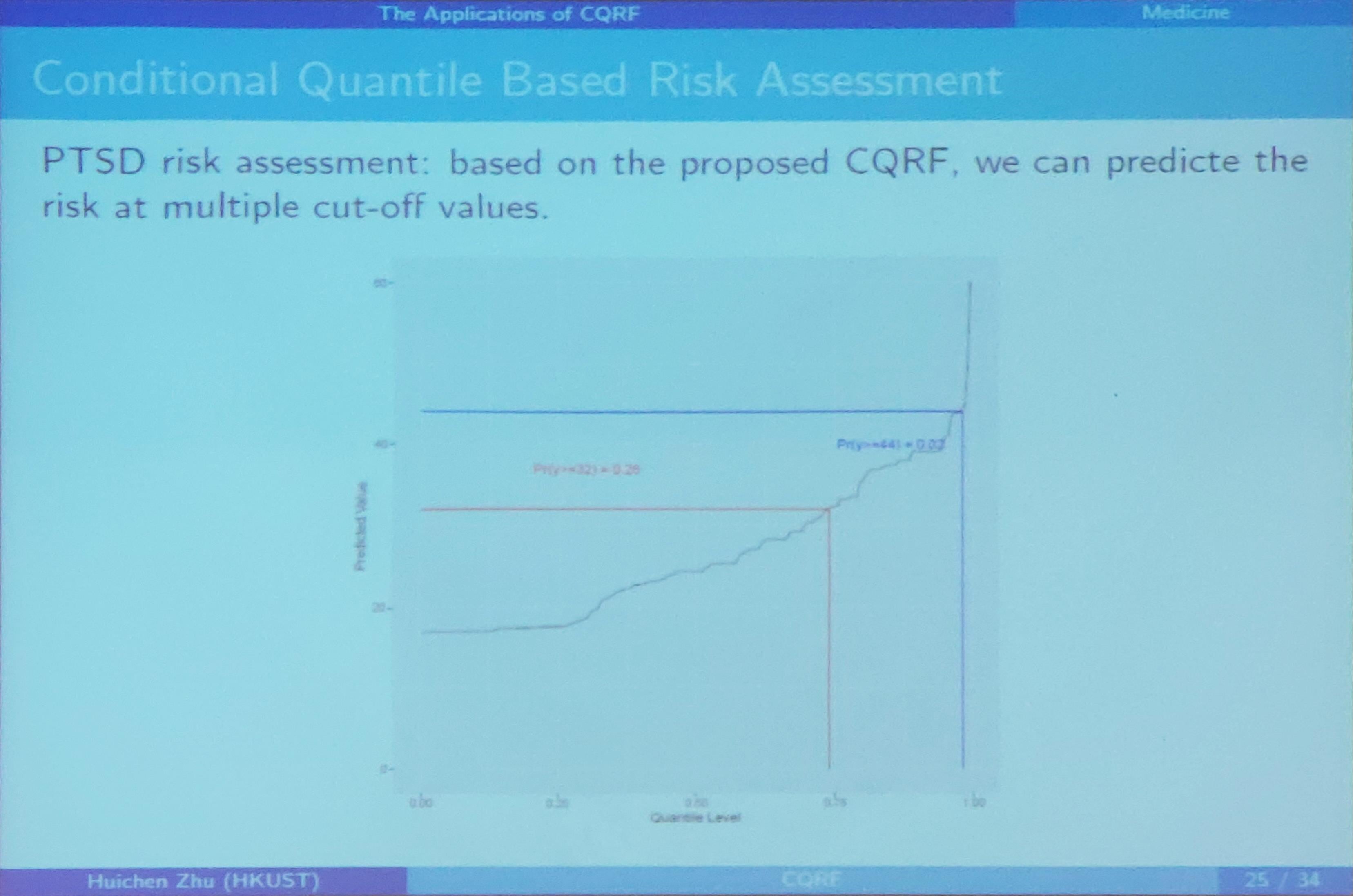
Conditional Quantile Regression Forests
December 12, 2019
This note is based on the slides of the seminar, Dr. ZHU, Huichen. Conditional Quantile Random Forest.
Lagrange Multiplier Test
December 17, 2019
This post is based on Peter BENTLER’s talk, S.-Y. Lee’s Lagrange Multiplier Test in Structural Modeling: Still Useful? in the International Statistical Conference in Memory of Professor Sik-Yum Lee.
DNA copy number profiling: from bulk tissue to single cells
January 02, 2020
This post is based on the talk given by Yuchao Jiang at the 11th ICSA International Conference on Dec. 20th, 2019.
Concentration Inequality for Machine Learning
January 09, 2020
This post is based on the material of the first lecture of STAT6050 instructed by Prof. Wicker.
Classification with Imperfect Training Labels
January 15, 2020
This post is based on the talk, given by Timothy I. Cannings at the 11th ICSA International Conference on Dec. 22th, 2019, the corresponding paper is Cannings, T. I., Fan, Y., & Samworth, R. J. (2019). Classification with imperfect training labels. ArXiv:1805.11505 [Math, Stat]
Multiple Isotonic Regression
February 20, 2020
The first two sections are based on a good tutorial on the isotonic regression, and the third section consists of the slides for the talk given by Prof. Cun-Hui Zhang at the 11th ICSA International Conference on Dec. 21st, 2019.
Bernstein-von Mises Theorem
February 24, 2020
I came across the Bernstein-von Mises theorem in Yuling Yao’s blog, and I also found a quick definition in the blog hosted by Prof. Andrew Gelman, although this one is not by Gelman. By coincidence, the former is the PhD student of the latter!
Common Principal Components
February 28, 2020
This post is based on Flury (1984).
Bootstrap Sampling Distribution
March 05, 2020
This note is based on Lehmann, E. L., & Romano, J. P. (2005). Testing statistical hypotheses (3rd ed). Springer.
Survey on Functional Principal Component Analysis
April 25, 2020
This post is based on Shang, H. L. (2014). A survey of functional principal component analysis. AStA Advances in Statistical Analysis, 98(2), 121–142.
Robust Forecasting by Functional Principal Component Analysis
April 25, 2020
This post is based on Hyndman, R. J., & Shahid Ullah, Md. (2007). Robust forecasting of mortality and fertility rates: A functional data approach. Computational Statistics & Data Analysis, 51(10), 4942–4956.
Internal migration and transmission dynamics of tuberculosis
April 30, 2020
Survey on Time Series Change Points
May 31, 2020
This note is based on the survey paper, Aminikhanghahi, S., & Cook, D. J. (2017). A Survey of Methods for Time Series Change Point Detection. Knowledge and Information Systems, 51(2), 339–367.
Noise Adaptive Group Testing
July 30, 2020
This note is for Cuturi, M., Teboul, O., Berthet, Q., Doucet, A., & Vert, J.-P. (2020). Noisy Adaptive Group Testing using Bayesian Sequential Experimental Design.
An objective comparison of cell-tracking algorithms
August 21, 2020
Global Tracking via the Viterbi Algorithm
August 27, 2020
Iterative Closest Point
November 07, 2020
This note is for Besl, P. J., & McKay, N. D. (1992). Method for registration of 3-D shapes. Sensor Fusion IV: Control Paradigms and Data Structures, 1611, 586–606..
Star Formation
March 13, 2021 0 Comments
This note is for Chapter 19 of Astronomy Today, 8th Edition.
Generalized Degrees of Freedom
May 03, 2021 0 Comments
This note is for Ye, J. (1998). On Measuring and Correcting the Effects of Data Mining and Model Selection. Journal of the American Statistical Association, 93(441), 120–131..
Multivariate Adaptive Regression Splines
May 10, 2021 0 Comments
This note is for Friedman, J. H. (1991). Multivariate Adaptive Regression Splines. The Annals of Statistics, 19(1), 1–67.
Hypothesis Testing on A Nuisance Parameter
May 11, 2021 0 Comments
This note is for DAVIES, R. B. (1987). Hypothesis testing when a nuisance parameter is present only under the alternative. Biometrika, 74(1), 33–43.
Permutation Tests and Randomization Tests
May 22, 2021 0 Comments
End-to-End Instance Segmentation
May 27, 2021 0 Comments
This note is for ISTR: End-to-End Instance Segmentation with Transformers.
Unsupervised Multi-granular Chinese Word Segmentation via Graph Partition
June 03, 2021 0 Comments
Word Segmentation and Medical Concept Recognition for Chinese Medical Texts
June 10, 2021 0 Comments
Summarize Medical Conversations
June 10, 2021 0 Comments
Biomedical Named Entity Recognition
June 10, 2021 0 Comments
Self-organized Maps of Document Collections
June 12, 2021 0 Comments
This note is for Kaski, S., Honkela, T., Lagus, K., & Kohonen, T. (1998). WEBSOM – Self-organizing maps of document collections
Knowledge Graph and Electronic Medical Records
June 29, 2021 0 Comments
This note covers several papers on Knowledge Graph and Electronic Medical Records.
Multiple Object Tracking via Minimizing Energy
July 05, 2021 0 Comments
Bayesian Sparse Multiple Regression
September 16, 2021 0 Comments
Exploring DNN via Layer-Peeled Model
September 25, 2021 0 Comments
Multiple Descent of Minimum-Norm Interpolants
October 11, 2021 0 Comments
Benign Overfitting in Linear Regression
October 11, 2021 0 Comments
This note is for Bartlett, P. L., Long, P. M., Lugosi, G., & Tsigler, A. (2020). Benign Overfitting in Linear Regression. ArXiv:1906.11300 [Cs, Math, Stat].
Bayesian Leave-One-Out Cross Validation
October 20, 2021 0 Comments
Asymptotic Properties of High-Dimensional Random Forests
November 09, 2021 0 Comments
Biclustering on Gene Expression Data
November 10, 2021 0 Comments
The note is based on Padilha, V. A., & Campello, R. J. G. B. (2017). A systematic comparative evaluation of biclustering techniques. BMC Bioinformatics, 18(1), 55.
Debiased ML via NN for GLM
November 16, 2021 0 Comments
Multidimensional Monotone Bayesian Additive Regression Tree
November 17, 2021 0 Comments
This note is for Chipman, H. A., George, E. I., McCulloch, R. E., & Shively, T. S. (2021). mBART: Multidimensional Monotone BART. ArXiv:1612.01619 [Stat].
Causal Inference by Invariant Prediction
November 19, 2021 0 Comments
Invariant Risk Minimization
November 19, 2021 0 Comments
This note is for Arjovsky, M., Bottou, L., Gulrajani, I., & Lopez-Paz, D. (2020). Invariant Risk Minimization. ArXiv:1907.02893 [Cs, Stat].
Regularization-Free Principal Curves
November 21, 2021
The note is for Gerber, S., & Whitaker, R. (2013). Regularization-Free Principal Curve Estimation. 18.
Probabilistic Principal Curves
November 22, 2021
This note is for Chang, K.-Y., & Ghosh, J. (2001). A unified model for probabilistic principal surfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence, 23(1), 22–41., but only involves the principal curves.
Review on Random Matrix Theory
December 01, 2021
This note is for Paul, D., & Aue, A. (2014). Random matrix theory in statistics: A review. Journal of Statistical Planning and Inference, 150, 1–29.
Asymptotics of Cross Validation
December 03, 2021
This note is for Austern, M., & Zhou, W. (2020). Asymptotics of Cross-Validation. ArXiv:2001.11111 [Math, Stat].
Additive Model with Linear Smoother
December 07, 2021
This note is for Buja, A., Hastie, T., & Tibshirani, R. (1989). Linear Smoothers and Additive Models. The Annals of Statistics, 17(2), 453–510. JSTOR.
Gaussian Processes for Regression
December 13, 2021
This note is for Chapter 4 of Rasmussen, C. E., & Williams, C. K. I. (2006). Gaussian processes for machine learning. MIT Press.
Generalizing Ridge Regression
December 14, 2021
This note is for Chapter 3 of van Wieringen, W. N. (2021). Lecture notes on ridge regression. ArXiv:1509.09169 [Stat].
Empirical Bayes
January 16, 2022
This note is based on Sec. 4.6 of Lehmann, E. L., & Casella, G. (1998). Theory of point estimation (2nd ed). Springer.
Neuronized Priors for Bayesian Sparse Linear Regression
January 16, 2022
This note is for Shin, M., & Liu, J. S. (2021). Neuronized Priors for Bayesian Sparse Linear Regression. Journal of the American Statistical Association, 1–16.
Leave-one-out CV for Lasso
March 14, 2022
This note is for Homrighausen, D., & McDonald, D. J. (2013). Leave-one-out cross-validation is risk consistent for lasso. ArXiv:1206.6128 [Math, Stat].
Applications with Scale Parameters
March 22, 2022
This note contains several papers related to scale parameter.
Equivariance
March 22, 2022
This post is for Chapter 3 of Lehmann, E. L., & Casella, G. (1998). Theory of point estimation (2nd ed). Springer.
Prediction Risk for the Horseshoe Regression
March 24, 2022
The note is for Bhadra, A., Datta, J., Li, Y., Polson, N. G., & Willard, B. (2019). Prediction Risk for the Horseshoe Regression. 39.
Scale Mixture Models
March 25, 2022
This note is for scale mixture models.
Mixture of Location-Scale Families
March 25, 2022
This note is for Chen, J., Li, P., & Liu, G. (2020). Homogeneity testing under finite location-scale mixtures. Canadian Journal of Statistics, 48(4), 670–684.
Adaptive Ridge Estimate
March 30, 2022
Big Data Paradox
April 07, 2022
Test of Monotonicity
April 20, 2022
This note is for Chetverikov, D. (2019). TESTING REGRESSION MONOTONICITY IN ECONOMETRIC MODELS. Econometric Theory, 35(4), 729–776.
Monotonicity in Asset Returns
April 20, 2022
Test of Monotonicity by U-processes
April 23, 2022
This note is for Ghosal, S., Sen, A., & van der Vaart, A. W. (2000). Testing Monotonicity of Regression. The Annals of Statistics, 28(4), 1054–1082.
Test of Monotonicity and Convexity by Splines
April 23, 2022
Monotone Multi-Layer Perceptron
July 04, 2022
This note is for monotonic Multi-Layer Perceptron Neural network, and the references are from the R package monmlp.
Review on Multi-omics Data
July 14, 2022
This note is based on Subramanian, I., Verma, S., Kumar, S., Jere, A., & Anamika, K. (2020). Multi-omics Data Integration, Interpretation, and Its Application. Bioinformatics and Biology Insights, 14, 1177932219899051.
Fitting to Future Observations
July 21, 2022
This note is for Jiang, Y., & Liu, C. (2022). Estimation of Over-parameterized Models via Fitting to Future Observations (arXiv:2206.01824). arXiv.
Debiased Inverse-Variance Weighted Estimator in Mendelian Randomization
September 20, 2022
This post is for the talk at Yale given by Prof. Ting Ye based on the paper Ye, T., Shao, J., & Kang, H. (2020). Debiased Inverse-Variance Weighted Estimator in Two-Sample Summary-Data Mendelian Randomization (arXiv:1911.09802). arXiv.
Contrastive Learning: A Simple Framework and A Theoretical Analysis
October 06, 2022
This note is based on
- Chen, T., Kornblith, S., Norouzi, M., & Hinton, G. (2020). A Simple Framework for Contrastive Learning of Visual Representations (arXiv:2002.05709). arXiv.
- Ji, W., Deng, Z., Nakada, R., Zou, J., & Zhang, L. (2021). The Power of Contrast for Feature Learning: A Theoretical Analysis (arXiv:2110.02473). arXiv.
Single-cell Graph Neural Network
October 08, 2022
This note is for Prof. Dong Xu’s talk on Wang, J., Ma, A., Chang, Y., Gong, J., Jiang, Y., Qi, R., Wang, C., Fu, H., Ma, Q., & Xu, D. (2021). ScGNN is a novel graph neural network framework for single-cell RNA-Seq analyses. Nature Communications, 12(1), Article 1.
ADAM and AMSGrad for Stochastic Optimization
October 09, 2022
This post is based on
- Kingma, D. P., & Ba, J. (2017). Adam: A Method for Stochastic Optimization (arXiv:1412.6980). arXiv.
- Reddi, S. J., Kale, S., & Kumar, S. (2018, February 15). On the Convergence of Adam and Beyond. International Conference on Learning Representations.
scDesign3: A Single-cell Simulator
October 10, 2022
This note is based on Jingyi Jessica Li’s talk on Song, D., Wang, Q., Yan, G., Liu, T., & Li, J. J. (2022). A unified framework of realistic in silico data generation and statistical model inference for single-cell and spatial omics (p. 2022.09.20.508796). bioRxiv.
Simultaneous Estimation of Cell Type Proportions and Cell Type-specific Gene Expressions
October 12, 2022
Bayesian Hierarchical Varying-Sparsity Regression Models with Application to Cancer Proteogenomics.
October 29, 2022
Integrative Bayesian Analysis of High-dimensional Multiplatform Genomics Data
October 30, 2022
Joint Bayesian Variable and DAG Selection
October 31, 2022
First Glance at KEGGgraph
November 21, 2022
This post is based on
- Zhang JD, Wiemann S (2022-11-01). KEGGgraph: a graph approach to KEGG PATHWAY in R and Bioconductor.
- Zhang JD (2022-11-01). KEGGgraph: Application Examples
Tutorial on Polygenic Risk Score
January 24, 2023
This note is based on Choi, S. W., Mak, T. S.-H., & O’Reilly, P. F. (2020). Tutorial: A guide to performing polygenic risk score analyses. Nature Protocols, 15(9), Article 9.
Predictive Degrees of Freedom
February 10, 2023
This note is for Luan, B., Lee, Y., & Zhu, Y. (2021). Predictive Model Degrees of Freedom in Linear Regression. ArXiv:2106.15682 [Math].
Model Selection for Cox Models with Time-Varying Coefficients
March 28, 2023
This note is for Yan, J., & Huang, J. (2012). Model Selection for Cox Models with Time-Varying Coefficients. Biometrics, 68(2), 419–428.
Cox Models with Time-Varying Covariates vs Time-Varying Coefficients
March 28, 2023
Age-dependency of PRS for Prostate Cancer
April 21, 2023
C-index for Time-varying Risk
May 05, 2023
This post is for Gandy, A., & Matcham, T. J. (2022). On concordance indices for models with time-varying risk (arXiv:2208.03213). arXiv.
Deep Generative Modeling for Single-cell Transcriptomics
June 29, 2023
Single Cell Generative Pre-trained Transformer
June 30, 2023
XGBoost for IPF Biomarker
July 10, 2023
Cluster Analysis of Transcriptomic Datasets of IPF
July 10, 2023
Cell type-specific and disease-associated eQTL in the human lung
July 13, 2023
scMDC: Single-cell Multi-omics Data Clustering Analysis
July 27, 2023
PseudotimeDE: Differential Gene Expression along Cell Pseudotime
July 27, 2023
tradeSeq: Trajectory-based differential expression analysis for single-cell sequencing data
July 31, 2023
Six Statistical Senses
August 28, 2023
This note is for Craiu, R. V., Gong, R., & Meng, X.-L. (2023). Six Statistical Senses. Annual Review of Statistics and Its Application, 10(1), 699–725.
In-Context Learning via Transformers
September 14, 2023
condiments: Trajectory Inference across Multiple Conditions
September 14, 2023
Confidence Intervals of Smoothed Isotonic Regression
September 21, 2023
This note is for Groeneboom, P., & Jongbloed, G. (2023). Confidence intervals in monotone regression (arXiv:2303.17988). arXiv.
Fast and Flexible methods for monotone polynomial fitting
September 21, 2023
Shape-Constrained Estimation Using Nonnegative Splines
September 21, 2023
An Iterative Procedure for Shape-constrained Smoothing using Smoothing Splines
September 21, 2023
This note is for Turlach, B. A. (2005). Shape constrained smoothing using smoothing splines. Computational Statistics, 20(1), 81–104.
Constrained Smoothing and Out-of-range Prediction using P-splines
September 22, 2023
scHOT: Investigate higher-order interactions in single-cell data
October 13, 2023
Consistent Probabilities along GO Structure
November 16, 2023
Hierarchical Multi-Label Classification
November 20, 2023
This post is for two papers on Hierarchical multi-label classification (HMC), which imposes a hierarchy constraint on the classes.
Hierarchical Multi-label Contrastive Learning
November 25, 2023
This post is for Zhang, Shu, Ran Xu, Caiming Xiong, and Chetan Ramaiah. “Use All the Labels: A Hierarchical Multi-Label Contrastive Learning Framework,” 16660–69, 2022.
Approximation to Log-likelihood of Nonlinear Mixed-effects Model
November 26, 2023
ClusterDE: a post-clustering DE method
December 04, 2023
Uncertainty of Pseudotime Trajectory
December 04, 2023
Exact Post-Selection Inference for Sequential Regression Procedures
January 19, 2024
Statistical Learning and Selective Inference
January 19, 2024
SuSiE: Sum of Single Effects Model
January 22, 2024
Fine-mapping from Summary Data with SuSiE
January 22, 2024
t-Test for Mixture Normal Data
January 23, 2024
Edgeworth Expansion
January 24, 2024
This note is based on Shao, J. (2003). Mathematical statistics (2nd ed). Springer. and Hwang, J. (2019). Note on Edgeworth Expansions and Asymptotic Refinements of Percentile t-Bootstrap Methods. Bootstrap Methods.
Contrasting Genetic Architectures using Fast Variance Components Analysis
February 07, 2024
Selective Inference for Hierarchical Clustering
February 08, 2024
This note is for Gao, L. L., Bien, J., & Witten, D. (2022). Selective Inference for Hierarchical Clustering (arXiv:2012.02936). arXiv.
Bipartitle eQTL Network Construction
February 08, 2024
Post-clustering Inference under Dependency
February 08, 2024
This post is for González-Delgado, J., Cortés, J., & Neuvial, P. (2023). Post-clustering Inference under Dependency (arXiv:2310.11822). arXiv.
BLiP: Bayesian Linear Programming
February 09, 2024
The note is for Spector, A., & Janson, L. (2023). Controlled Discovery and Localization of Signals via Bayesian Linear Programming (arXiv:2203.17208). arXiv.
Comparisons of transformations for single-cell RNA-seq data
March 26, 2024
This post is for Ahlmann-Eltze, C., & Huber, W. (2023). Comparison of transformations for single-cell RNA-seq data. Nature Methods, 20(5), 665–672.
Selective Inference for K-means
April 12, 2024
This note is for Chen, Y. T., & Witten, D. M. (2022). Selective inference for k-means clustering (arXiv:2203.15267). arXiv.
Test Difference for A Single Feature
April 12, 2024 0 Comments
This note is for Chen, Y. T., & Gao, L. L. (2023). Testing for a difference in means of a single feature after clustering (arXiv:2311.16375). arXiv.
Conditional Independence Test in Single-cell Multiomics
April 17, 2024 0 Comments
This note is for Boyeau, P., Bates, S., Ergen, C., Jordan, M. I., & Yosef, N. (2023). Calibrated Identification of Feature Dependencies in Single-cell Multiomics.