WeiYa's Work Yard

A dog, who fell into the ocean of statistics, tries to write down his ideas and notes to save himself.

M-estimator

Posted on (Update: )
Tags: M-estimator

Let $M_n$ be random functions and let $M$ be a fixed function of $\theta$ such that for every $\varepsilon > 0$

\[\begin{align*} \sup_{\theta\in\Theta} & \vert M_n(\theta) - M(\theta)\vert \pto 0\\ \sup_{\theta:d(\theta,\theta_0)\ge \varepsilon} &M(\theta) < M(\theta_0)\,. \end{align*}\]

Then any sequence of estimators $\hat\theta_n$ with $M_n(\hat\theta_n)\ge M_n(\theta_0)-o_P(1)$ converges in probability to $\theta_0$.

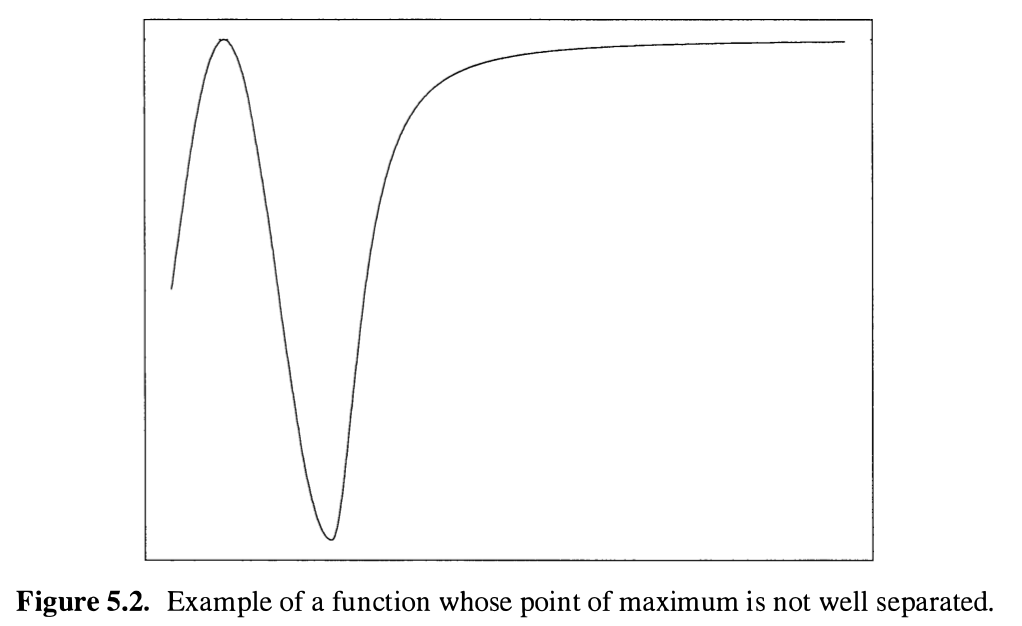
The first condition says that the sequence $M_n$ converges to a nonrandom map $M:\Theta \rightarrow \bar\IR$, and the second condition requires that this map attains its maximum at a unique point $\theta_0$, and only parameters close to $\theta_0$ may yield a value of $M(\theta)$ close to the maximum value $M(\theta_0)$. Thus, $\theta_0$ should be a well-separated point of maximum of $M$, and a counterexample is the following figure,

Pay attention to the $o_P(1)$ in the inequality, bear in mind that it is a short for a sequence of random vectors that converges to zero in probability.

Let $\Psi_n$ be random vector-valued functions and let $\Psi$ be a fixed vector-valued functions of $\theta$ such that for every $\varepsilon > 0$

\[\begin{align*} \sup_{\theta\in\Theta} & \Vert \Psi_n(\theta) - \Psi(\theta)\Vert \pto 0\\ \inf_{\theta :d(\theta,\theta_0)\ge\varepsilon} & \Vert \Psi(\theta)\Vert > 0 = \Vert \Psi(\theta_0)\Vert\,. \end{align*}\]

Then any sequence of estimators $\hat\theta_n$ such that $\Psi_n(\hat\theta_n)=o_P(1)$ converges in probability to $\theta_0$.

Let $\Theta$ be a subset of the real line and let $\Psi_n$ be random functions and $\Psi$ a fixed function of $\theta$ such that $\Psi_n(\theta)\rightarrow \Psi(\theta)$ in probability for every $\theta$. Assume that each map $\theta\mapsto \psi\Psi_n(\theta)$ is continuous and has exactly one zero $\hat\theta_0$, or is nondecreasing with $\Psi_n(\hat \theta_n)=o_P(1)$. Let $\theta_0$ be a point such that $\Psi(\theta_0-\varepsilon) < 0 < \Psi(\theta_0+\varepsilon)$ for every $\varepsilon > 0$.

Let $X_1,\ldots,X_n$ be a sample from some distribution $P$, and let a random and a “true” criterion function be of the form:

\[\Psi_n(\theta) = \frac 1n\sum_{i=1}^n \psi_\theta(X_i)=\bbP_n\psi_\theta,\quad \Psi(\theta) = P\psi_\theta\,.\]

Assume that the estimator $\hat\theta_0$ is a zero of $\Psi_n$ and converges in probability to a zero $\theta_0$ of $\Psi$. Because $\hat\theta_n\rightarrow\theta_0$, expand $\Psi_n(\hat\theta_n)$ in a Taylor series around $\theta_0$. Assume for simplicity that $\theta$ is one-dimensional, then

\[0 = \Psi_n(\hat\theta_n) = \Psi_n(\theta_0) + (\hat\theta_n-\theta_0)\dot\Psi_n(\theta_0) + \frac 12(\hat\theta_n-\theta_0)^2\ddot\Psi_n(\tilde \theta_n)\,,\]

where $\tilde \theta_n$ is a point between $\hat\theta_n$ and $\theta_0$. This can be rewritten as

\[\sqrt n(\hat\theta_n-\theta_0) = \frac{-\sqrt n\Psi_n(\theta_0)}{\dot\Psi_n(\theta_0)+\frac 12(\hat\theta_n-\theta_0)\ddot\Psi_n(\tilde \theta_n)}\,.\] \[\sqrt{n}(\hat\theta_n-\theta_0) \rightarrow N\left(0, \frac{P\psi_{\theta_0}^2}{(P\dot\psi_{\theta_0})}\right)\] \[\sqrt{\hat\theta_n-\theta_0}\rightarrow N_k\left(0, (P\dot\psi_{\theta_0})^{-1}P\psi_{\theta_0}\psi_{\theta_0}^T(P\dot\psi_{\theta_0})^{-1}\right)\]

here the invertibility of the matrix $P\dot\psi_{\theta_0}$ is a condition.

For each $\theta$ in an open subset of Euclidean space, let $x\mapsto \psi_\theta(x)$ be a measurable vector-valued function such that, for every $\theta_1$ and $\theta_2$ in a neighborhood of $\theta_0$ and a measurable function $\dot\psi$ with $P\dot\psi^2<\infty$ and that the map $\theta\mapsto P\psi_\theta$ is differentiable at a zero $\theta_0$, with nonsingular derivative matrix $V_{\theta_0}$. If $\bbP_n\psi_{\hat\theta_n}=o_P(n^{-1/2})$, and $\hat\theta_n\pto \theta_0$, then $$ \sqrt n(\hat\theta_n-\theta_0) = -V_{\theta_0}^{-1}\frac{1}{\sqrt n}\sum_{i=1}^n\psi_{\theta_0}(X_i)+o_P(1)\,, $$ In particular, the sequence $\sqrt n(\hat\theta_n-\theta_0)$ is asymptotically normal with mean zero and covariance matrix $V_{\theta_0}^{-1}P\psi_{\theta_0}\psi_{\theta_0}^T(V_{\theta_0}^{-1})^T$.

The function $\theta\mapsto \sign(x-\theta)$ is not Lipschitz, the Lipschitz condition is apparently still stronger than necessary.

For each $\theta$ in an open subset of Euclidean space let $x\mapsto m_\theta(x)$ be a measurable function such that $\theta\mapsto m_\theta(x)$ is differentiable at $\theta_0$ for $P$-almost every $x$ with derivative $\dot m_{\theta_0}(x)$ and such that, for every $\theta_1$ and $\theta_2$ in a neighborhood of $\theta_0$ and a measurable function $\dot m$ with $P\dot m^2<\infty$ $$ \vert m_{\theta_1}(x) - m_{\theta_2}(x)\vert \le \dot m(x) \Vert \theta_1-\theta_2\Vert\,. $$ Furthermore, assume that the map $\theta\mapsto Pm_\theta$ admits a second-order Taylor expansion at a point of maximum $\theta_0$ with nonsingular symmetric second derivative matrix $V_{\theta_0}$. If $\bbP m_{\hat\theta_n}\ge \sup_\theta\bbP_nm_\theta - o_P(n^{-1})$ and $\hat\theta_n\pto \theta_0$, then $$ \sqrt n(\hat\theta_n-\theta_0) = -V_{\theta_0}^{-1}\frac{1}{\sqrt n}\sum_{i=1}^n\dot m_{\theta_0}(X_i) +o_P(1)\,. $$ In particular, the sequence $\sqrt n(\hat\theta_n-\theta_0)$ is asymptotically normal with mean zero and covariance matrix $V_{\theta_0}^{-1}P\dot m_{\theta_0}\dot m_{\theta_0}^TV_{\theta_0}^{-1}$.

Median

Misspecified Model

Published in categories Note 
← previous    next →

See all posts →