Global data association for MOT using network flows
Posted on
This note is based on Li Zhang, Yuan Li, & Nevatia, R. (2008). Global data association for multi-object tracking using network flows. 2008 IEEE Conference on Computer Vision and Pattern Recognition, 1–8.
Define data association as a MAP problem. The problem is then mapped into a cost-flow network, and solved with a min-cost flow algorithm.
Basis of the mapping: there is an analogy between finding non-overlapping object trajectories and finding edge-disjoint paths in a graph.
MAP under non-overlap constraints
- $\x_i=(x_i,s_i,a_i,t_i)$: detection response
- $\calX=\{\x_i\}$: a set of object observations
- $T_k=\{\x_{k_1},\ldots,\x_{k_{l_k}}\}$: a single trajectory hypothesis
- $\calT=\{T_k\}$: an association hypothesis, a set of single trajectory hypotheses.
(differ time ? time increasing ??)
The objective of data association is to maximize the posterior probability of $\calT$ given the observation set $\calX$:
\[\cT^* = \argmax_{\cT}P(\cT\mid \cX) = \argmax_{\cT}P(\cX\mid \cT)P(\cT)=\argmax_{\cT}\prod_iP(\x_i\mid \cT)P(\cT)\]Reduce the search space by using the observation that one object can only belong to one trajectory:
\[\cT_k\cap \cT_l = \emptyset,\forall k\neq l\,.\]Assume the motion of each object is independent,
\[\begin{align*} \cT^* &= \argmax_{\cT}\prod_{i}P(\x_i\mid\cT)\prod_{\cT_k\in \cT}P(\cT_k)\\ & s.t. \cT_k\cap \cT_l=\emptyset,\forall k\neq l\,. \end{align*}\]A Bernoulli distribution is used to model the cases of an observation being a true detection as well as being a false alarm ($\beta_i$ is the probability for $\x_i$ being a false alarm):
\[P(\x_i\mid\cT) = \begin{cases} 1-\beta_i & \exists T_k\in \cT,\x_i\in \cT_k\\ \beta_i & \text{otherwise} \end{cases}\]$P(\cT_k)$ is modeled as a Markov chain, which includes initialization probability $P_{entr}$, termination probability $P_{exit}$, and transition probabilities $P_{link}(\x_{k_i+1}\mid \x_{k_i})$:
\[P(\cT_k) = P_{entr}(\x_{k_0})P_{link}(\x_{k_1}\mid \x_{k_0})P_{link}(\x_{k_2}\mid \x_{k_1})\cdots P_{link}(x_{k_{l_k}}\mid x_{k_{l_k}-1})P_{exit}(\x_{k_{l_k}})\](still not global?)
\[P_{link}(\x_j\mid \x_i) = P(s_j\mid x_i,s_i,\Delta t)P(x_j\mid x_i,\Delta t)P(a_j\mid a_i)P(\Delta t)\] \[P(\Delta t) = \begin{cases} Z_t \alpha^{\Delta t-1} & 1\le \Delta t\le \xi\\ 0 & \Delta t < 1 or \Delta t > \xi \end{cases}\]Min-cost flow solution

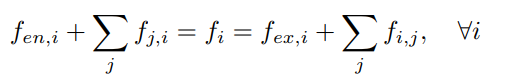

This formulation can be mapped into a cost-flow network $G(\cX)$ with source $s$ and sink $t$.
Given an observation set $\cX$:
for every observation $\x_i\in \cX$,
- create two nodes $u_i,v_i$,
- create an arc $(u_i, v_i)$ with cost $c(u_i,v_i)=C_i$ and flow $f(u_i,v_i)=f_i$
- an arc $(s, u_i)$ with cost $c(s,u_i)=C_{en,i}$ and flow $f(s, u_i)=f_{en,i}$
- an arc $(v_i, t)$ with cost $c(v_i,t)=C_{ex,i}$ and flow $f(v_i, t)=f_{ex,i}$
for every transition $P_{link}(\x_j\mid \x_i)\neq 0$,
- create an arc $(v_i, u_j)$ with cost $c(v_i, u_j)=C_{i,j}$ and flow $f(v_i,u_j)=f_{i,j}$.
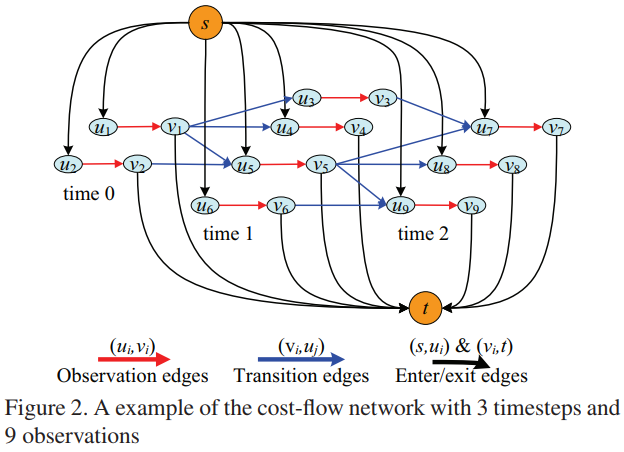
- each flow path can be interpreted as an object trajectory
- the amount of the flow sent from $s$ to $t$ is equal to the number of object trajectories
- the total cost of the flow on $G$ corresponds to the (negative) log-likelihood of the association hypothesis
- the flow conservation constraint guarantees that no flow paths share a common edge
The optimal cost should be calculated over all possible $f(G)$, which is the amount of flow sent from source to sink.
