In-Context Learning via Transformers
Posted on
In-context learning: the ability of a model to condition on a prompt sequence consisting of in-context samples along with a new query point, and generate the corresponding output.
While large language models such as GPT3 exhibit some ability to perform in-context learning, it is unclear what the relationship is between tasks on which this succeeds and what is present in the training data.
The paper consider the well-defined problem of training a model to in-context learn a function class (e.g., linear functions): that is, given data derived from some functions in the class, can we train a model to in-context learn “most” functions from this class?
The paper empirically shows that standard Transformers can be trained from scratch to perform in-context learning of linear functions.
- $D_\cX$: the distributions over inputs
- $D_\cF$: a distribution over functions in $\cF$
- prompt $P$: a sequence $(x_1, f(x_1),\ldots, x_k, f(x_k), x_{query})$ where inputs ($x_i$ and $x_{query}$) are drawn iid from $D_\cX$ and $f$ is drawn from $D_\cF$
say a model $M$ can in-context learn the function class $\cF$ up to $\epsilon$, w.r.t. $(D_\cF, D_\cX)$, if it can predict $f(x_{query})$ with an average error
\[\bbE_P[\ell(M(P), f(x_{query}))] \le \epsilon\]
Their findings:
- Transformers can in-context learn linear functions
- $D_\cX$ is an isotropic Gaussian in 20 dimensions
- $D_\cF$: linear functions with weight vectors drawn from an isotropic Gaussian
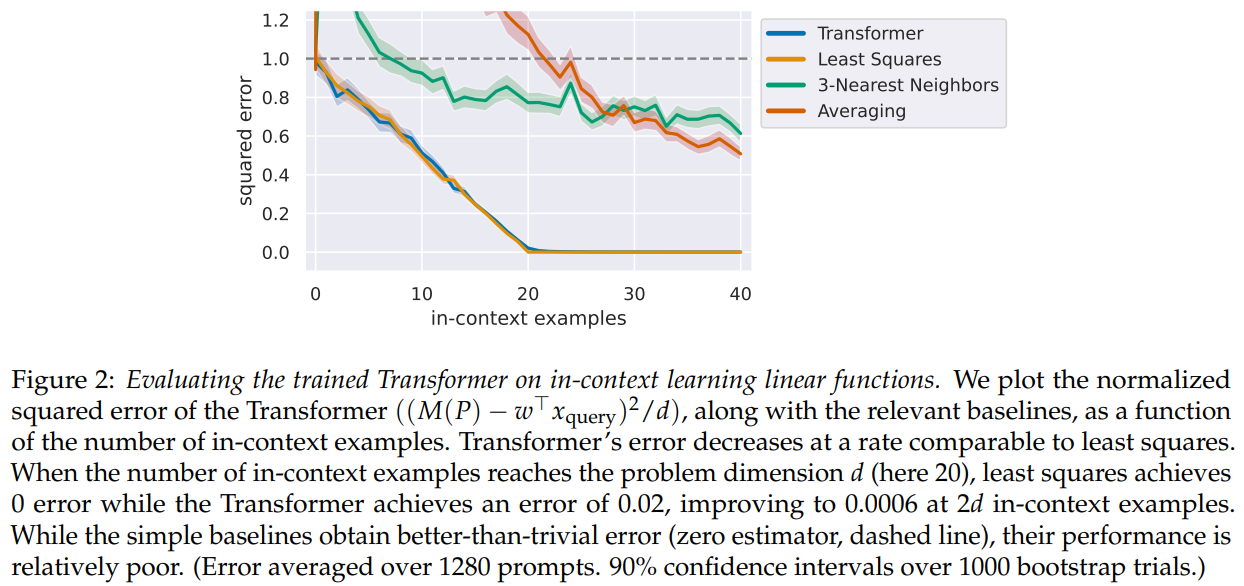

- Generalization to out-of-distribution prompts

- More complex function classes

- Role of model capacity and problem dimension
