CFPCA for Human Movement Data
Posted on (Update: )
The functional principal components (FPCs) for each group are
- either determined separately (yielding components that are group-specific),
- The group-specific FPCs contain both within and between group variation and issue arise when comparing FPCs across groups when the order of the FPCs alter in each group.
- or by combing the data for all groups and determining the FPCs of the combined data (yielding components that summerize the entire data set).
- The FPCs of the combined data may not adequately describe all groups of individuals and comparisons between groups typically use $t$-tests of the mean FPC scores in each group.
Aim to perform FPCA in a manner allowing sensible comparisons between groups of curves. CFPCA identifies the common sources of variation evident across groups but allows the order of each component to change for a particular group. This allows for the direct comparison of components across groups.
Introduction
Aim of Human movement research studies: determine differences in movement patterns between several groups of individuals,
- differences between injured and control subjects
- differences between athletes grouped according to skill level
- differences between children at various developmental stages
- changes in movement patterns in response to some intervention
A need for a suitable method which allows for a comparison of the variance structure across treatment groups. The common functional principal component analysis determines the modes of variation that are common to each group but allows the ordering of the components to change across groups. This enables the direct comparison of variation patterns across groups.
The eigenvalues determine the ranking of the CFPCs in each group and examining these rankings places the emphasis on comparing differences in the distribution of the variation across the factors in each group rather than comparing the means.
Data
Three groups:
- AT(O): The injured subjects (AT group) were observed wearing customized orthoses
- AT(NO): The injured subjects (AT group) were not wearing customized orthoses
- the control group (uninjured subjects)
CFPCA for Independent groups: AT(NO) vs control
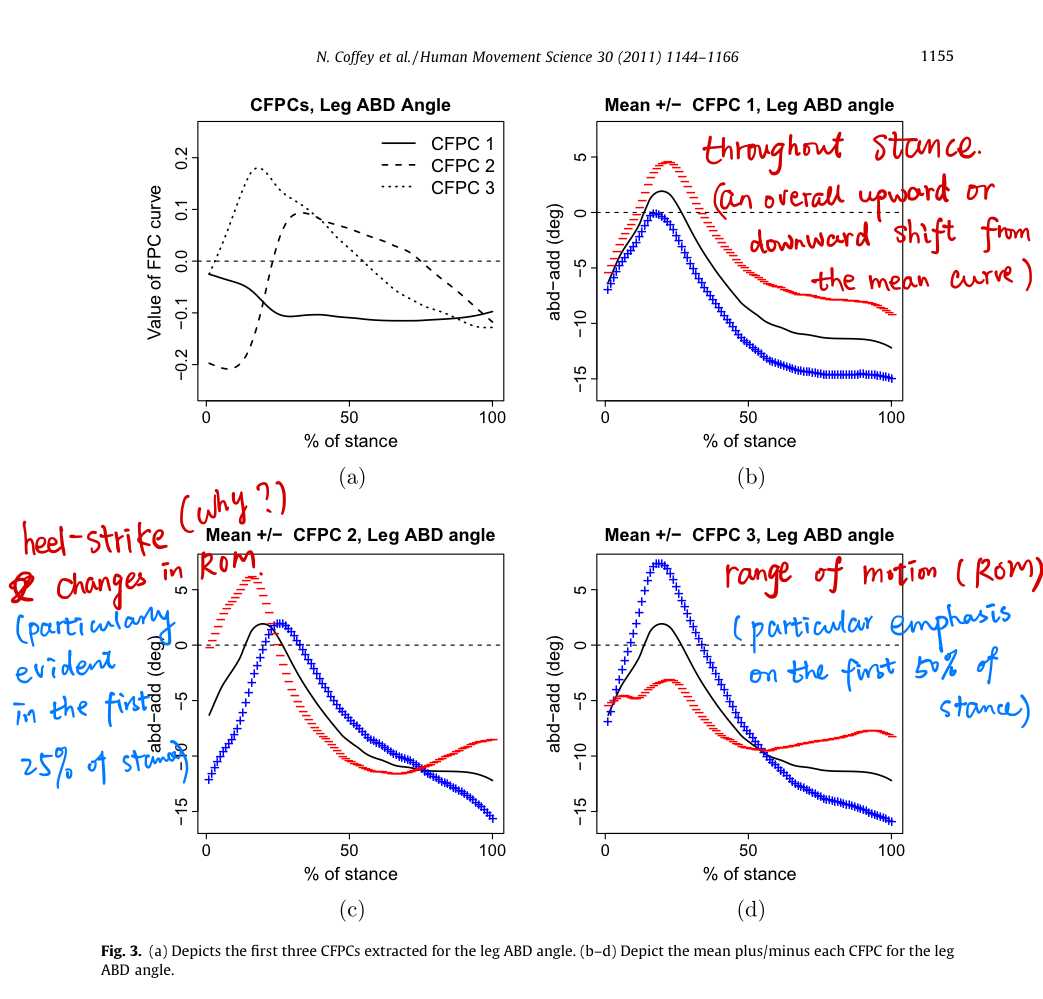
Compare the different based on the proportions of the explained variance of the common PCs, such as
- over 90% of the variation in control subjects can be explained by changes in leg ABD throughout stance but only 69% of the variation in injured subjects can be explained by changes in leg ABD throughout stance.
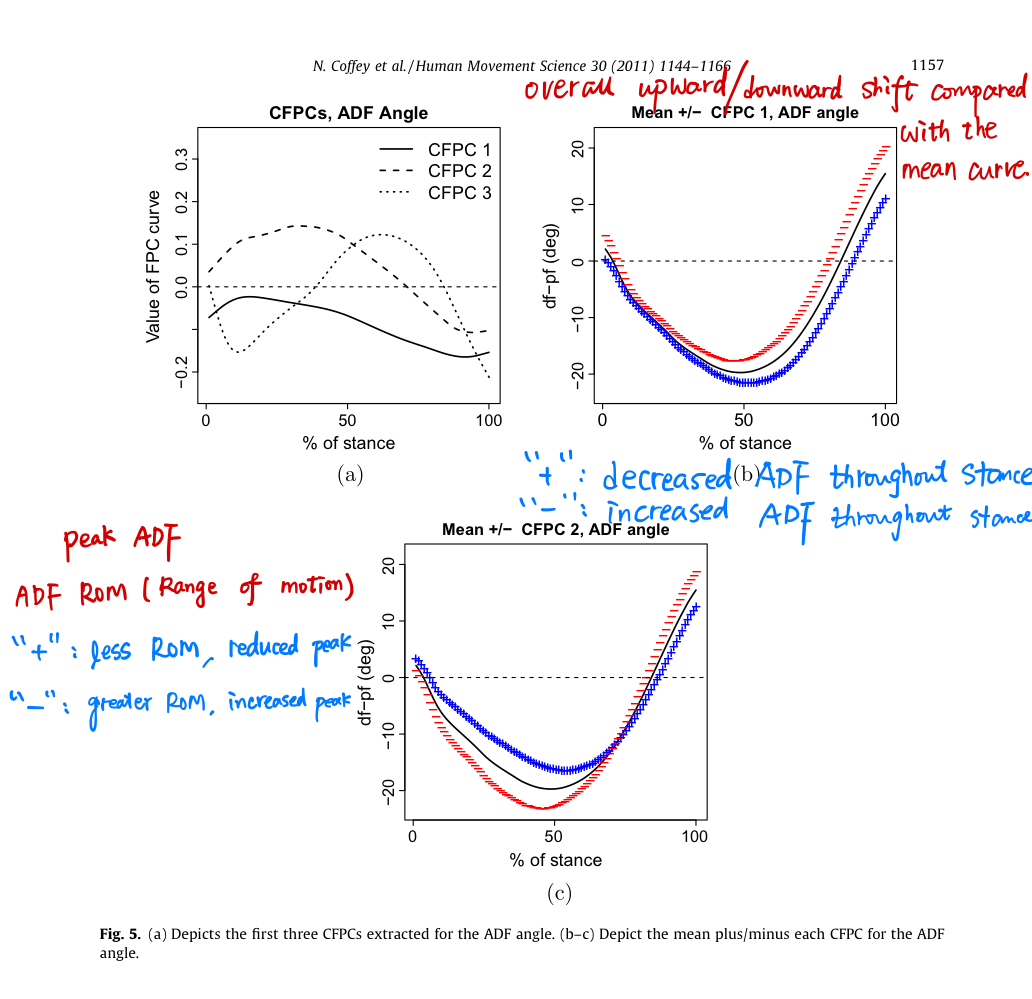
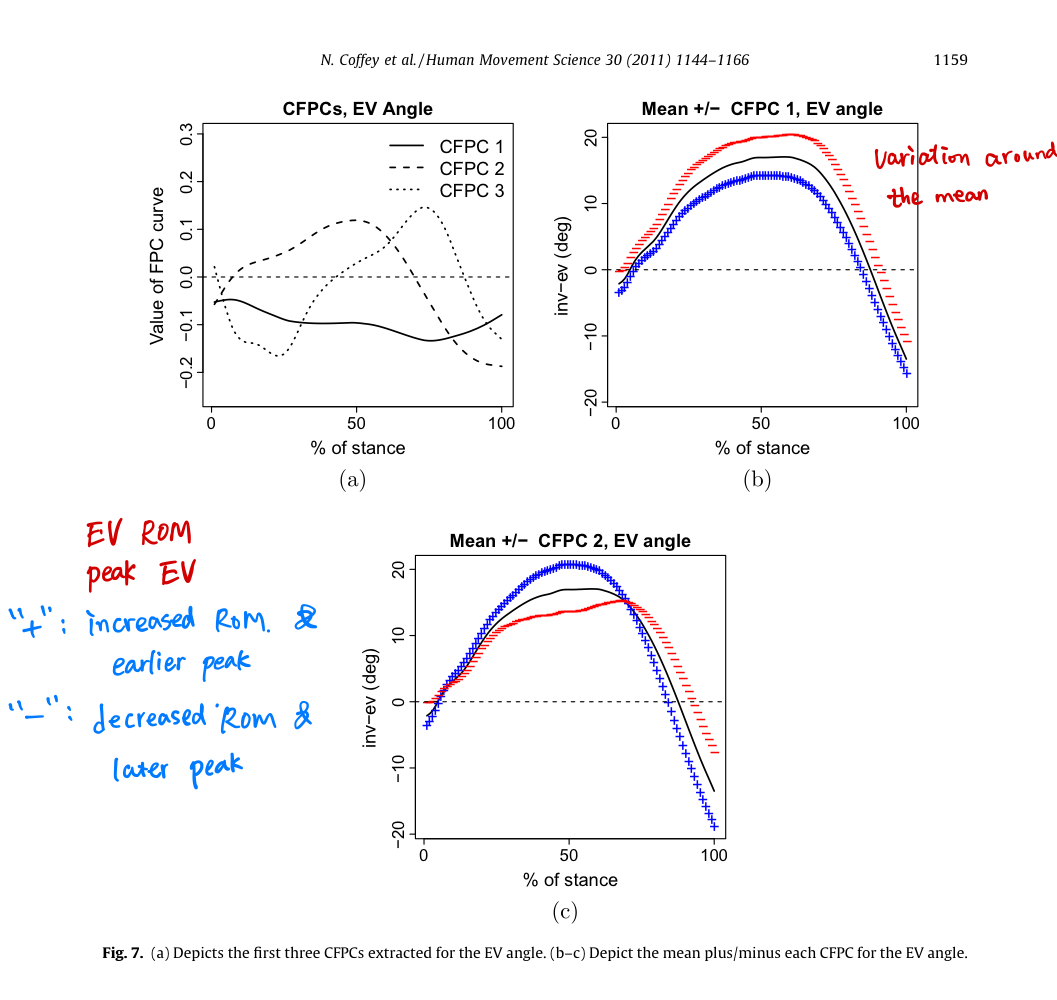
DCFPCA for Dependent groups: AT(O) vs AT(NO)
DCFPCA is similar to CFPCA as it assumes that some rotation simultaneously diagonalizes the within-group covariance functions and that all groups share the same components. However DCFPCA also requires that the same rotation diagonalizes the cross-covariance functions of measurements between groups.
\[\gamma_{g_1g_2}(s,t) = \Delta^c(s)\Lambda_{g_1g_2}^c\Delta^{cT}(t)\,,\]where the $\Lambda_{g_1g_2}^c$ values determine the ranking of each component both within and between groups. (a little confused, does it need to consider $g_1=g_2$, or only $g_1\neq g_2$? Different from the CFPCA, the eigenvalues would be calculated for each group, and should only determine the ranking of the component within group. Both within and between groups is something similar to the FPCA for the aggregated data set.)
Discussion
While FPCA (and comparisons of the average scores) examines changes in average behavior across groups, CFPCA and DCFPCA examine changes in variability across groups. The CFPCA methodology places the emphasis on comparing the changes in patterns of variation across groups by extracting the common modes of variation and examining the group-specific eigenvalues. The method shows that although the same factors may influence the variation across groups, the distribution of the variation across these factors can be different.