Common Principal Components
Posted on
This post is based on Flury (1984).
In the situation of the same variables being measured on objects from different groups, the covariance structure may vary from group to group. And in some these cases, tests of significance suggest that the underlying population covariance matrices are not exactly identical in all groups.
Yet sometimes the covariance matrices of different groups look somehow similar, and it seems reasonable to assume that the covariance matrices have a common basic structure:
- proportionality of the covariance matrices: Rao (1982)
- some rotation diagonalizes the covariance matrices simultaneously in all populations: this paper
Mathematically, $k (p\times p)$-covariance matrices $\Sigma_1,\ldots, \Sigma_k$ is expressed by the hypothesis
\[H_C:\beta'\Sigma_i\beta = \Lambda_i \text{diagonal}\quad i=1,\ldots,k\,,\]where $\beta$ is an orthogonal $p\times p$ matrix.
- $H_C$: hypothesis of common PC’s
- $U_i = \beta’X_i$: common principal components (CPC’s)
In contrast to the one-sample PCA, no canonical ordering of the columns of $\beta$ need be given, since the rank order of the diagonal elements of the $\Lambda_i$ is not necessarily the same for all groups.
Assume $\X_i\iid N_p(\u_i, \Sigma_i)$, and let $\S_i$ be te usual unbiased sample covariance matrices for samples of size $N_i=n_i+1$. Then the matrices $n_i\S_i$ are independently distributed as $W_p(n_i,\Sigma_i)$, and the common likelihood function of $\Sigma_1,\ldots,\Sigma_k$ given $\S_1,\ldots,\S_k$ is
\[L(\Sigma_1,\ldots,\Sigma_k) = C\times \prod_{i=1}^k\mathrm{etr}\left(-\frac{n_i}{2}\Sigma_i^{-1}S_i\right)\vert \Sigma_i\vert^{-n_i/2}\,.\]Maximizing the likelihood function is equivalent to minimizing
\[g(\Sigma_1,\ldots,\Sigma_k) = \sum_{i=1}^k n_i(\log \vert \Sigma_i\vert + \tr\Sigma_i^{-1}\S_i)\]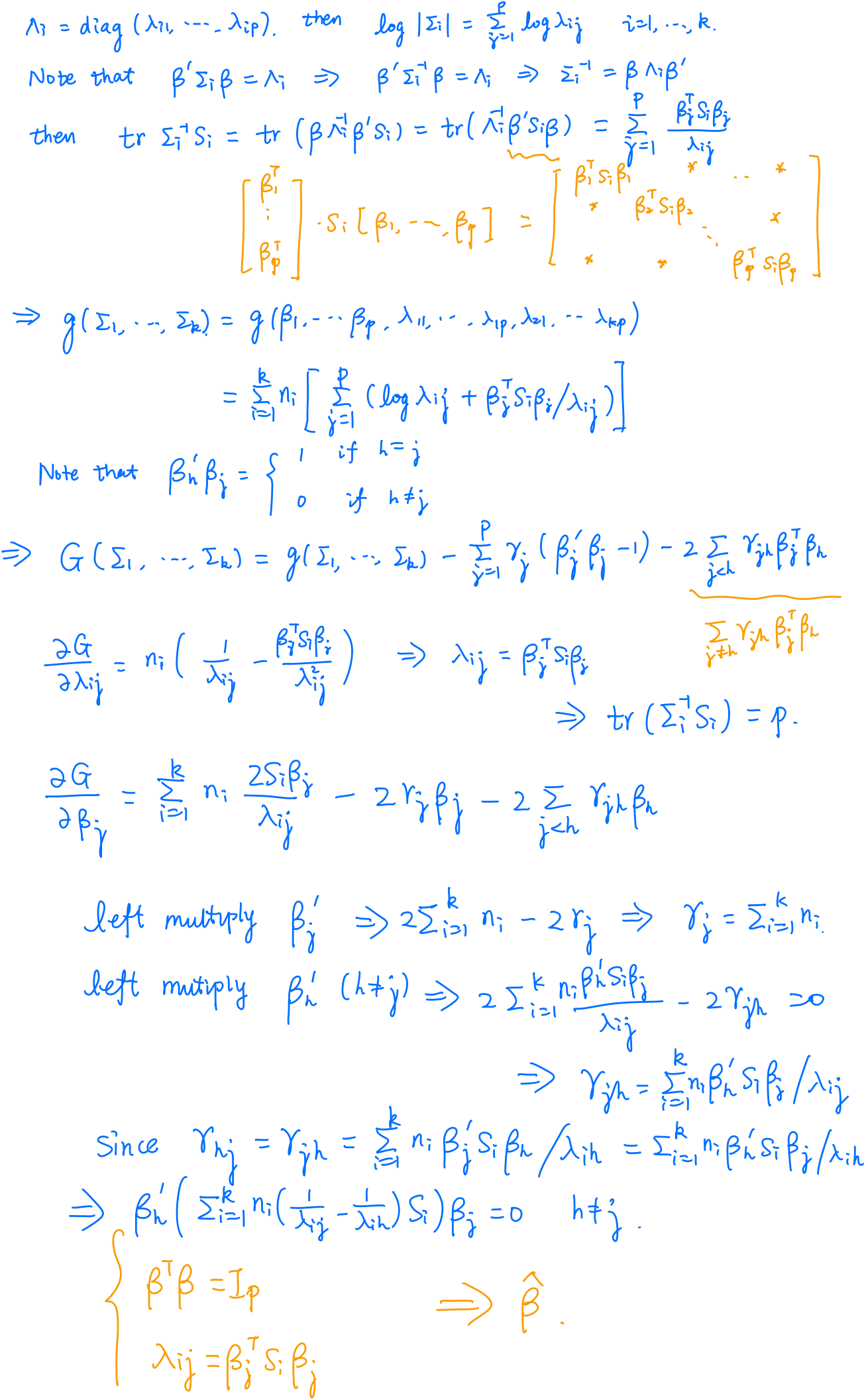
Properties
The weight of matrix $\S_i$ is $n_i\frac{\lambda_{ih}-\lambda_{ij}}{\lambda_{ij}\lambda_{ih}}$, and note that $\lambda_{ij}$ is the variance of the linear combination $\beta_j’\X_i$. If $\lambda_{ij} = \lambda_{ih}$, then $\S_i$ disappears from the $(h,j)$-th equation, which corresponds to sphericity of $\X_i$ in the plane spanned by $\beta_j$ and $\beta_h$.