Multivariate Mediation Effects

Posted on Nov 04, 2019 (Update: Dec 03, 2019)

Tags: Mediation Analyses, Intersection-union Test, DNA Methylation

This note is based on Huang, Y.-T. (2019). Variance component tests of multivariate mediation effects under composite null hypotheses. Biometrics, 0(0).

Scientific question

• In the US, socioeconomic disadvantage is positively associated with adiposity (肥胖症)
• Socioeconomic disadvantage is associated with DNA methylation (甲基化)
• DNA methylation is associated with adiposity

The author states their hypothesis as

\[\text{Socioeconomic status $\rightarrow$ DNA methylation $\rightarrow$ BMI}\,.\]

DNA methylation

DNA甲基化是在DNA甲基化转移酶(Dnmt)的作用下将甲基选择性地添加到胞嘧啶上形成5-胞嘧啶的过程，刚被发现时被定义为第五种碱基，实际上它是一种重要的表观遗传学标记，在调控基因表达、维持染色质结构、基因印记、X染色体失活以及胚胎发育等生物学过程中发挥着重大的作用。它就像DNA的一顶最神奇的“帽子”，带给世人层出不穷的惊喜…

DNA甲基化与表观遗传学

过去人们一直以为遗传和环境两大因素共同决定生物体的性状，然而人们无法合理解释马和驴的正反交后代、同卵双胞胎差别以及x染色体失活等现象。1942年Waddington首次提出了表观遗传学(epigenetics)的概念，它针对研究基因型与表型的关系，使经典的孟德尔核内遗传规律无法解释的现象得到了合理而完美的解释。基因组表观遗传修饰主要包括DNA甲基化修饰与核小体中组蛋白的修饰等，使得被修饰DNA的空间结构发生改变或使染色体结构发生改变，导致基因的沉默或过度表达。这两种修饰都是在不改变DNA碱基种类与数量的前提下使生物体表型呈现出多样化。DNA甲基化对基因表达模式以及基因组稳定性均起着至关重要的作用，并在印迹基因与x染色体失活等典型的表观遗传现象中起重要作用。

refer to 徐浩明@知乎

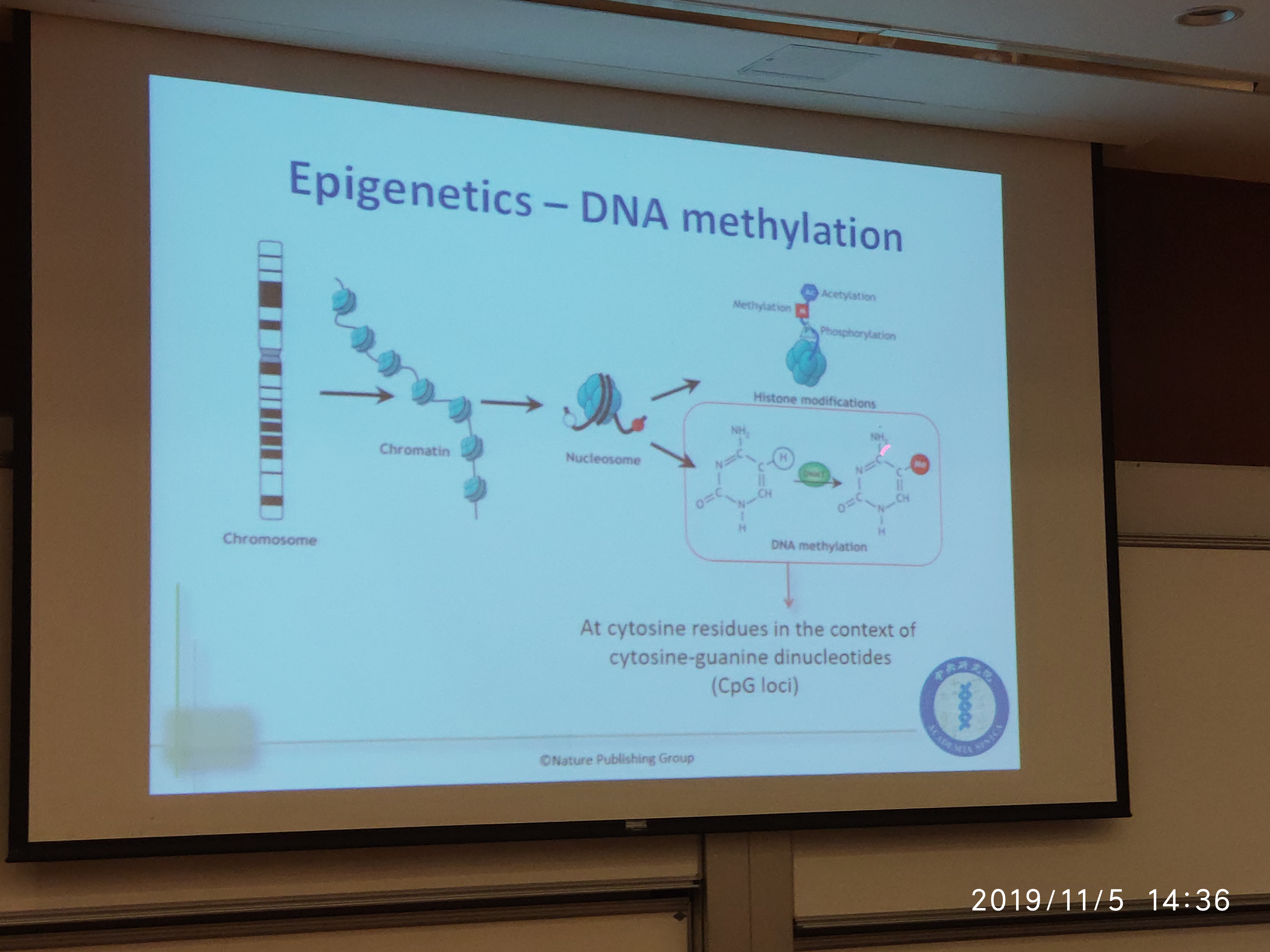
• Chromatin: 染色质
• histone modification: 组蛋白修饰
• Nucleosome: 染色质核小体
• Acetylation: 乙酰化
• Phosphorylation： 〔化〕氧化磷酸化作用
• cytosine: 【生化】胞(核)嘧啶
• guantine: 【化】鸟嘌呤
• dinucleotides: 双碱基脱氧核糖核酸

Dataset: NEFS

The New England Family Study (NEFS) is a longitudinal investigation aimed at identifying obstetric and genetic risk factors for neuropsychiatric (神经精神病学的) and other medical disorders with developmental origins, including schizophrenia (精神分裂症), bipolar (双相型障碍的；躁狂抑郁性精神病的) and major affective disorders, substance use, learning disabilities, attention-deficit/hyperactivity (注意缺陷多动症) disorder (ADHD) and cardiovascular (心血管的) disease. This historic project is a follow-up study to the National Collaborative Perinatal Project (NCPP), which was conducted during the 1960s in twelve cities throughout the United States. A community-based birth-cohort study, the original NCPP enrolled and followed about 60,000 pregnant women and their children. The children, followed from birth through age 7, were assessed periodically for physical and mental health status and a series of cognitive, behavioral and social outcomes. A wealth of data was generated from this study; hundreds of articles have been published on a wide range of topics regarding health and development.

The primary goal of the current study is to improve understanding of the effects of pregnancy and birth complications on neuropsychiatric disorders, and ultimately, to improve preventive and intervention efforts with these disorders. Previously known as the Harvard-Brown Collaborative Project, the title “New England Family Study” (NEFS) originated in the year 2000, and refers to the collective activities currently being conducted with the NCPP cohort in Boston and Providence . The new name was chosen to reflect the collaborative relationship of the two sites, easily identify the study group, and foster a sense of membership and pride among cohort participants. This unique cohort offers a rare opportunity for epidemiological investigation into neuropsychiatric and medical disorders; with the help of cohort members, the NEFS will continue this longitudinal follow-up study of health and development for years to come.

source: Mission Statement of NEFS

Causal Mediation Model

mediation: the state in which an exposure or an intervention affects an outcome through an intermediate variable, that is, the mediator.

• Baron and Kenny (1986): first propose a statistical approach to mediation analysis for a single-mediator model using a difference model
• Rubin (1978): further generalize the theory underlying the mediation analysis through a counterfactural outcome framework (?)
• the counterfactural approach extends the mediation analysis to various nonlinear models for dichotomous outcomes and survival outcomes with censoring
• the mediation analysis has advanced toward the setting with multiple mediators

Different from the socioeconomic in the seminar, the paper considers whether the effect of cigarette smoking on gene expression is mediated by affecting the epigenetic DNA methylation of the gene.

Conduct a gene-centric analysis where analyze one gene at a time and for each gene, set up a multimediator model with

• the exposure: cigarette smoking intensity
• the mediators: DNA methylation markers
• the outcome: mRNA expression of the gene

While literature of causal mediation analyses is more about estimation, this paper focuses on hypothesis testing, which is less studied in causal inference literature but important in application such as genome-wide analyses.

• MacKinnon et al. (2002): conduct comprehensive simulation studies to compare the type I error rate and statistical power of various existing tests for the single-mediator model
• Zhao et al. (2014): propose an efficient testing procedure for the marginal mediation effect and illustrate its genomic application
• Huang and Pan (2016): propose to examine both element-wise and marginal mediation effects when the number of mediators $p$ is larger than the sample size $n$ using a series of single-mediator models
• Barfield et al. (2017): in the setting with a large number of tests, hypothesis tests without considering the composite null are likely to be conservative when the true effect in a study is very sparse. Huang (2019) proposes a procedure to account for the null composition to address the issue.
• However, Huang (2019) focuses on tests with only one mediator, and how to conduct a large number of multimediator tests under the composite null hypothesis remains unclear. The paper aims to develop a testing procedure that adjusts for the null composition based on score tests of variance components for the multimediation effect.

Formulation and Assumptions

• $S$: smoking pack-years (or socioeconomic status in the seminar)
• $\M$: DNA methylation values of CpG loci within a gene
• $Y$: mRNA expression of the gene
• $\X$: covariates

For a subject $i=1,\ldots,n$, assume the following model for a gene $j$ that contains the DNA methylation marker $k, k=1,\ldots,p_j$, where $p_j$ is the total number of markers within the gene $j$:

\[\begin{align*} M_{ijk} &= \alpha_{Xjk}^T\X_i + \alpha_{Sjk}S_i + \varepsilon_{Mijk}\\ g(E[Y_{ij}\mid \X_i, S_i, \M_{ij}]) &= \beta_{Xj}^T\X_i + \beta_{Sj}S_i + \beta_{Mj}^T\M_{ij} \end{align*}\]

where

• $Y_{ij}$ follows a distribution in the exponential family
• $\varepsilon_{Mij} = (\varepsilon_{Mij1},\ldots,\varepsilon_{Mijp_j})^T$ follows a $p_j$ dimension multivariate normal with mean zeros and a covariance $\Sigma_j$.
• $g(\cdot)$: monotone link function

Define

• $Y(s, \m)$: the counterfactual outcome (??) $Y$ has the exposure $S$ and the mediators $\M$ been set to $s$ and $\m$, respectively
• $\M(s)$: the counterfactual mediator value had $S$ been set to $s$

Assumptions for identifiability of mediation:

• $Y(s)\ind S\mid \X$: no unmeasured confounding for the association of $Y$ and $S$
• $Y(s, \m)\ind \M\mid (\X, S)$: no unmeasured confounding for the association of $Y$ and $\M$ given $S$
• $M(s)\ind S\mid \X$: no unmeasured confounding for the association of $\M$ and $S$
• $Y(s, \m)\ind \M(s^*)\mid \X$: no $S$-induced confounder for the $\M$-$Y$ association.

Under the above assumptions, the marginal mediation effect of gene $j$ for $S=s_1$ vs. $s_0$ defined as

\[\Delta = E[Y(s_1, \M(s_1))\mid \X] - E[Y(s_1, \M(s_0))\mid \X]\,.\]

The null hypothesis, $H_0:\Delta=0$ is equivalent to the composite null hypothesis:

\[H_0:\alpha_S=0\cup \beta_M=0\]

Two special case where the marginal mediation effect $\Delta = 0$ under $\alpha_S\neq 0$ and $\beta_M\neq 0$.

• perfect cancellation of the element-wise mediation effects
• the disjoint effect

Single mediator & Single test

\[\begin{xy} \xymatrix@1{ A \ar[r]^{\hat\alpha_S} \ar@/^1cm/[rr] & B \ar[r]^{\hat \beta_M} & C } \end{xy}\]

• Mediation (indirect) effect: $\hat \alpha_S\hat\beta_M$
• Sobel (1982): $\Var(\hat\alpha_S)=\sigma_{\alpha n}^2, \Var(\hat\beta_M)=\sigma_{\beta n}^2$, \(\frac{\hat \alpha_S\hat \beta_M}{\sqrt{\hat\beta_M^2\sigma_{\alpha n}^2 + \hat \alpha_S^2\sigma_{\beta n}^2 }}\rightarrow N(0,1)\,.\)

Note that $\Var(X\cF) = \E[\Var(X\mid \cF)] + \Var[\E(X\mid \cF)]$

Existing tests for mediation

Let

\[\begin{align*} a(\alpha_S) &= \frac{\sqrt n(\hat \alpha_S-\alpha_S)}{\sqrt n \sigma_{\alpha n}}\\ b(\beta_M) &= \frac{\sqrt n(\hat \beta_M-\beta_M)}{\sqrt n\sigma_{\beta n}} \end{align*}\]

be the test statistics for $\hat \alpha_S$ and $\hat\beta_M$ given that

\[\begin{align*} \sqrt n(\hat \alpha_S-\alpha_S) & \rightarrow N(0, \sigma_\alpha^2)\\ \sqrt n(\hat \beta_M-\beta_M) & \rightarrow N(0, \sigma_\beta^2)\,. \end{align*}\]

• Normality-based test (Sobel’s test):

\[p_N = 2\Phi\left(-\frac{\vert ab\vert}{\sqrt{a^2+b^2}}\right)\]

• Normal product-based test under the alternative (?? how to under the alternative)

\[p_{NP1} = \int_{-\infty}^0 F_{z_1z_2}(t)dt\,,\]

where $z_1\sim N(\vert a\vert, 1)$ and $z_2\sim N(\vert b\vert, 1)$.

• Bootstrap test:

\[p_B = \frac 2B\sum_b I(\vert \hat \alpha_S^{(b)}\hat\beta_M^{(b)}\vert > 0)\]

• Joint significance test:

\[p_{JT} = 2\times \max(\Phi(-\vert a\vert), \Phi(-\vert b\vert))\]

• Normal product-based test centered at 0:

\[p_{NP0}=F(ab)\,,\]

where

\[F(z) = 2\int_{-\infty}^\infty \int_{\vert z/x\vert}^\infty \frac{1}{2\pi}e^{-\frac{x^2+y^2}{2}}dydx\,.\]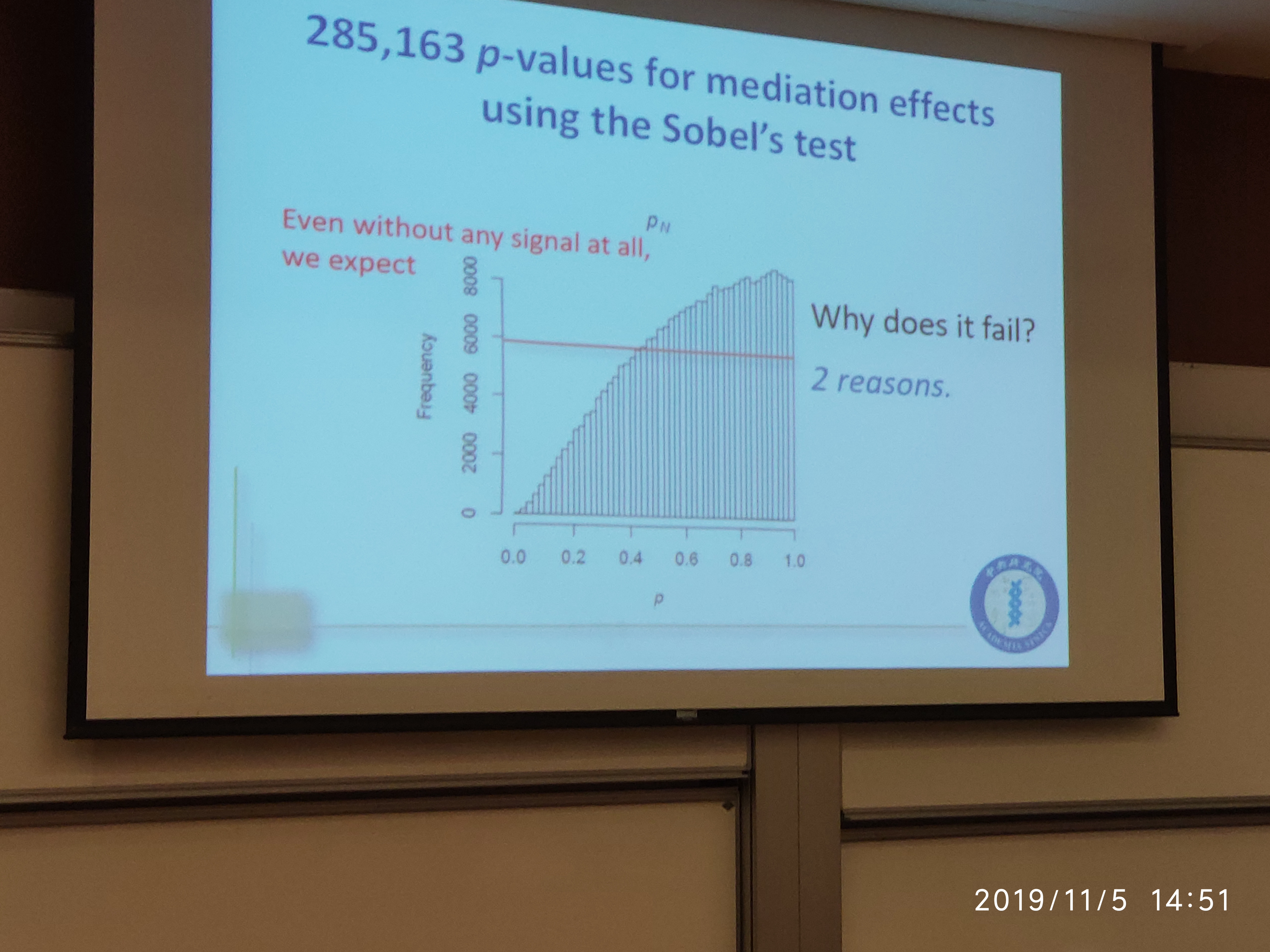

Restate the Model

\[\begin{align*} h(E(Y_i\mid \X_i,S_i,\M_i)) &= \X_i^T\beta_X + S_i\beta_S + \M_i^T\beta_M\\ \M_i &= A\X_i+S_i\alpha_S + \epsilon_{Mi} \end{align*}\]

where

• $Y$: BMI
• $S$: socioeconomic status
• $\M$: a set of DNA methylation values
• $\epsilon_{Mi}\sim MVN(0, \Sigma)$

The mediation effect is

\[ME = E[Y(s_1, M(s_1))\mid X] - E[Y(s_1, M(s_0))\mid X] = c(s_1-s_0)\alpha_S^T\beta_M\,.\]

There exists some problems:

• $p > n$
• $M_1, \ldots, M_p$ can be highly correlated

With the dimension reduction techniques, we can get

\[ME \propto \alpha_S^T\beta_M = {\alpha_S^*}^T\beta_M^* = \sum_j \alpha_{Sj}^*\beta_{Mj}^*\,.\]

In the testing procedure, let

• ${\theta^*}^T = ({\alpha_S^*}^T, {\beta_M^*}^T)$
• ${\hat\theta^*}^T = ({\hat\alpha_S^*}^T, {\hat\beta_M^*}^T)$

then the test statistics under the transformation model is

• Total mediation: $\hat\Delta^* = \Delta^*(\hat\theta^*)={\hat\alpha_S^*}^T{\hat\beta_M^*}$
• Element-wise mediation: $\hat\delta^* = \delta^*(\hat\theta^*)={\hat\delta_j^*\equiv (\hat\alpha_{Sj}^*\hat\beta_{Mj}^*),j=1,\ldots,p}$
• Variance of element-wise mediation: $\hat\tau_p = \tau_p(\hat\theta^*)=\big \vert \vert \delta^*(\hat\theta^*)\vert \big \vert^2$

Joint significance test (JT)

Two conclusions:

• The p-value of joint significance test $p_{JT}$ is smaller than that of normality-based test, $p_N$ and normal product-based test, $p_{NP1}$.
• The joint significance test is an intersection-union test (IUT) with a size $\alpha$.

the null hypothesis is that

for $p=2$,

To conduct multivariate joint significance test:

• Perform a two-sided $z$-test on $\frac{\vert \hat\alpha_S^T\hat\beta_M\vert }{\sqrt{V_\max}}$, where $V_\max = \max({w^*}^T\Sigma_nw^*)$ over $2^p$ combinations of $w_j$.
• Let $ \Sigma_n =\begin{bmatrix} \Sigma_{\alpha n} & 0\
  0 & \Sigma_{\beta n} \end{bmatrix}\,, $ and $w=(w_1,\ldots, w_p)^T, w_j\in\{\hat\alpha_{Sj},\hat\beta_{Mj}\}$, $w^*=(w_1^*,\ldots, w_p^*,w_{p+1}^*,\ldots,w_{2p}^*)^T$, where
  • if $w_j = \hat \alpha_{Sj}$, then $w_j^*=0$ and $w_{p+j}^*=\hat\beta_{Mj}$
  • if $w_j = \hat \beta_{Mj}$, then $w_j^*=\hat\alpha_{Sj}$ and $w_{p+j}^* = 0$

path-specific effect

Composite Null Hypothesis

Assume a composite null hypothesis:

• $H_0^{(1)}$ with probability $\pi_0$, $a\sim N(0, 1), b\sim N(0,1)$
• $H_0^{(2)}$ with probability $\pi_a$, $a\sim N(\mu_a, 1), b\sim N(0, 1)$
• $H_0^{(3)}$ with probability $\pi_b$, $a\sim N(0, 1), b\sim N(\mu_b, 1)$
• $\mu_a \sim N(0, \sigma_a^2)$ and $\mu_b\sim N(0, \sigma_b^2)$

then the $p$-value for testing the above null is

\begin{equation}\label{eq:pvalue} \pi_0F(ab) + \pi_a\int F(ab;\mu_a)d\Phi(\mu_a/\sigma_a) + \pi_b\int F(ab; \mu_b)d\Phi(\mu_b/\sigma_b) \end{equation}

Suppose $X$ has distribution $P_\theta$ for some $\theta\subset \Theta$, and the null hypothesis $H$ specifies $\theta\in \Omega_H$. Assume the rejection regions satisfy $S_\alpha \subset S_{\alpha’}$ if $\alpha < \alpha’$, then

• If $\sup_{\theta\in \Omega_H}P_\theta(X\in S_\alpha)\le \alpha$ for all $0 < \alpha < 1$, then the distribution of $\hat p$ under $\theta\in \Omega_H$ satisfies $P_\theta(\hat p\le u) \le u$ for all $0 \le u\le 1$.
• If for $\theta\in \Omega_H$, $P_\theta(X\in S_\alpha) = \alpha$ for all $0 < \alpha <1$, then $P_\theta(\hat p\le u)=u$ for all $0 \le u\le 1$; i.e., $\hat p$ is uniformly distributed over $(0, 1)$.

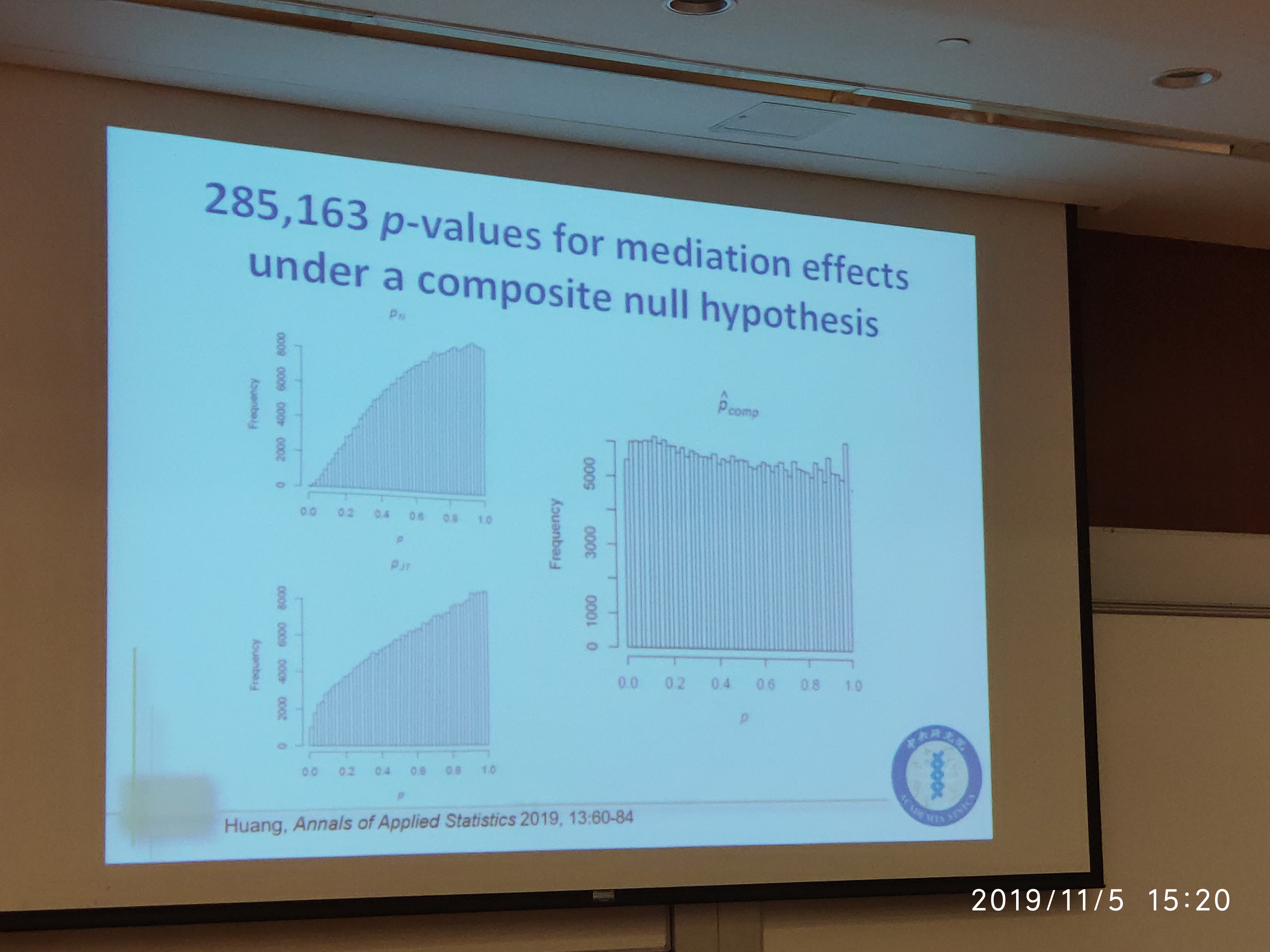
After the seminar, I asked a question related about the distribution of $p$-value. In my opinion and understanding for the above theorem, $p$-value not necessarily follows a uniform distribution under the composite null. The author explained that, under his assumption \eqref{eq:pvalue}, it indeed follows the uniform distribution. Then I doubt the justice for the comparison between his method with others’ nonuniform results since other paper may not require such assumption, but he still said others also satisfy such assumptions. I am not very convinced about his explanation.

Other related papers

1. Huang, Y.-T., & Pan, W.-C. (2016). Hypothesis test of mediation effect in causal mediation model with high-dimensional continuous mediators. Biometrics, 72(2), 402–413.
2. Huang, Y.-T. (2018). Joint significance tests for mediation effects of socioeconomic adversity on adiposity via epigenetics. The Annals of Applied Statistics, 12(3), 1535–1557.
3. Huang, Y.-T. (2019). Genome-wide analyses of sparse mediation effects under composite null hypotheses. The Annals of Applied Statistics, 13(1), 60–84.