One Parameter Models
Posted on
What is one-parameter model
A class of sampling distributions that is indexed by a single unknown parameter.
The binomial model
Happiness data
$n = 129$ individuals
If happiness, $Y_i = 1$, otherwise, $Y_i=0$.
A uniform prior distribution
\[p(\theta\vert y_1,\ldots, y_{129})\propto p(y_1,\ldots,y_{129}\vert\theta)\]Data and posterior distribution
\[p(y_1,\ldots,y_{129}\vert\theta)=\theta^{118}(1-\theta)^{11}\]An important formula:
\[\int_0^1\theta^{a-1}(1-\theta)^{b-1}d\theta=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}\]The beta distribution
\[p(\theta)=dbeta(\theta,a,b)=\frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\theta^{a-1}(1-\theta)^{b-1}\qquad \text{for }0\le \theta\le 1\]Three properties:
- $mode(\theta)=\frac{a-1}{a-1+b-1}$
- $E(\theta)=\frac{a}{a+b}$
- $Var(\theta)=\frac{E(\theta)E(1-\theta)}{a+b+1}$
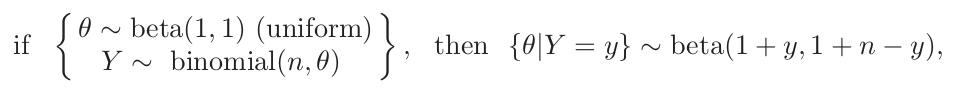
Confidence regions
Frequentist coverage lacks a post-experimental interpretation.
relationship
an interval that has 95% Bayesian coverage additionally has the property that
\[Pr(l(Y) < \theta < u(Y)\vert \theta) = .95+\epsilon_n\]where $\vert \epsilon_n\vert<a/n$
quantile-based interval
$n=10$ conditionally independent draws of a binary random variable.
using a uniform prior distribution for $\theta$
a = 1; b = 1 ## prior
n = 10; y =2 ## data
qbeta(c(.025, .975), a+y, b+n-y)
## 0.06021773 0.51775585
Hightest posterior density region
There is a simple R code which can return the HPD region.
The Poisson Model
\[Pr(Y=y\mid \theta)=dpois(y,\theta)=\theta^ye^{-\theta}/y!\quad \text{for }y\in \{0,1,2,\ldots,\}\]Two properties
- $E(Y\mid\theta)=\theta$
- $Var(Y\mid \theta)=\theta$
Gamma distribution
gamma(a,b)
\[p(\theta)=dgamma(\theta,a,b)=\frac{b^a}{\Gamma(a)}\theta^{a-1}e^{-b\theta}\]- $E(\theta) = a/b$
- $Var(\theta) = a/b^2$
- $mode(\theta)=(a-1)/b (if\;a > 1\;or\; 0)$
posterior distribution of $\theta$
Exponential families and conjugate priors
A one-parameter exponential family model is any model whose densities can be expressed as
\[p(y\mid\phi)=h(y)c(\phi)e^{\phi t(y)}\]conjugate prior distribution
\[p(\phi\mid n_0,t_0)=\kappa (n_0,t_0)c(\phi)^{n_0}e^{n_0t_0\phi}\]