Dynamics of Helicobacter pylori Infection

Posted on Sep 01, 2017 0 Comments

Tags: Helicobacter pylori, Differential Equations

The note is for Kirschner, D. E., & Blaser, M. J. (1995). The dynamics of helicobacter pylori infection of the human stomach. Journal of Theoretical Biology, 176(2), 281–290.

Abstract

1. Helicobacter pylori is a bacterial pathogen of the gastrointestinal tract (胃肠道) of humans causing chronic superficial gastritis (胃炎) which persists for decades.
2. The paper proposes a model for describing the interactions of H. pylori with its host, involving an autoregulatory network in which inflammation leads to nutrient release.
3. A determinist mathematical model examining the interactions necessary to maintain chronic infection indicates that this proposed autoregulatory network can produce steady-state solutions, and the model is robust in encompassing biological variations.

Introduction

1. three major constraints limiting bacteria’s number:
   • peristalsis
   • microbial competition
   • specific immune effectors

2. auto-regulatory feedback is the ability of H. pylori to persist. A mathematical model created to explore the theoretical construct indicates that the proposed feedback network produces the observed steady-state solutions.

3. persistence us may not be simple. Bacterial adherence is a strategy for resisting peristalsis, since the mucus layer in which most H. pylori reside is washed away due to peristalsis （蠕动）. Since adherence to the epithelial cells is beneficial, H. pylori migrates from the mucus to adhere to these cells. Since the adherent H. pylori divide, and the carrying capacity of the issue is most likely near saturation, most daughter cells must migrate into the mucus layer. Thus, assume bi-directional migration

4. it is the $A$ population which serves to sustain the infection, and the $M$ population is present to replenish $A$ and for transmission to new hosts.

5. As you can see in the figure, bacteria elaborate pro-inflammatory (促炎症) effectors provoking host responses leading to tissue damage with consequent nutrient release.

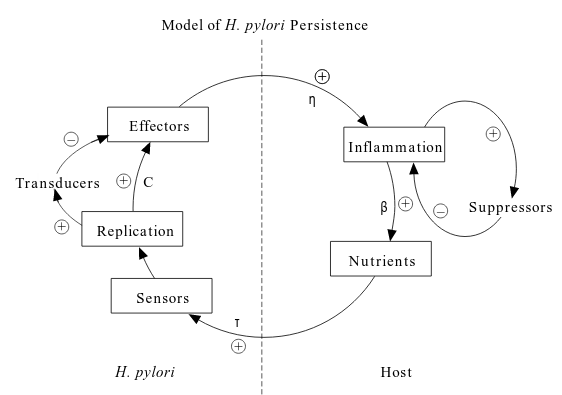
Model

Four population are defined and their interactions are formulated using differential equations describing their rates of change,

• $M(t)$: the concentration of H. pylori in the mucus layer at ant time
• $A(t)$: the concentration of H. pylori adherent to the epithelial cells
• $N(t)$: the nutrients
• $E(t)$: the effectors

\[\frac{dM}{dt} = ...\] \[\frac{dA}{dt} = ...\] \[\frac{dN}{dt} = ...\] \[\frac{dE}{dt} = ...\]

Analytical Results

1. the steady-state system that occurs when all the derivatives are equal to zero was examined, permitting each of the equations to be solved for the respective populations. It is not possible to solve explicitly for the respective populations in terms of the parameters alone.
2. It is possible to solve for population $M$ as a function of the parameters and population $A$.

Parameter Estimation

1. The remainder of the parameters $(c, \beta, \tau, \eta)$ relate to the interactions of effectors and nutrients. We can predict the ranges of values through numerical studies.

Competition

1. Two strain of H. pylori give rise to two different free-living mucus and adherent populations, $M1(t)$, and $A1(t)$ and $M2(t)$ and $A2(t)$.

Biological Variations

1. Some exogenous stimuli such as aspirin intake or smoking may alter the epithelial cells and hence change the carrying capacity.

Can A Simpler Model Work?

1. the steady-state cannot be reached in vivo in this scenario.

Discussion

1. This system was designed to model the steady-state condition, which exists for the majority of H. pylori residence in the human stomach.
2. The characteristics of the initial events and the long-term decline in bacterial numbers are beyond the scope of this report.