Identifiability and Estimability
Posted on
Materials from STAT 5030.
To parameterize $\bmu=\E\bY$ is to write $\bmu$ as a function of some parameters: $\bmu = f(\bbeta)$.
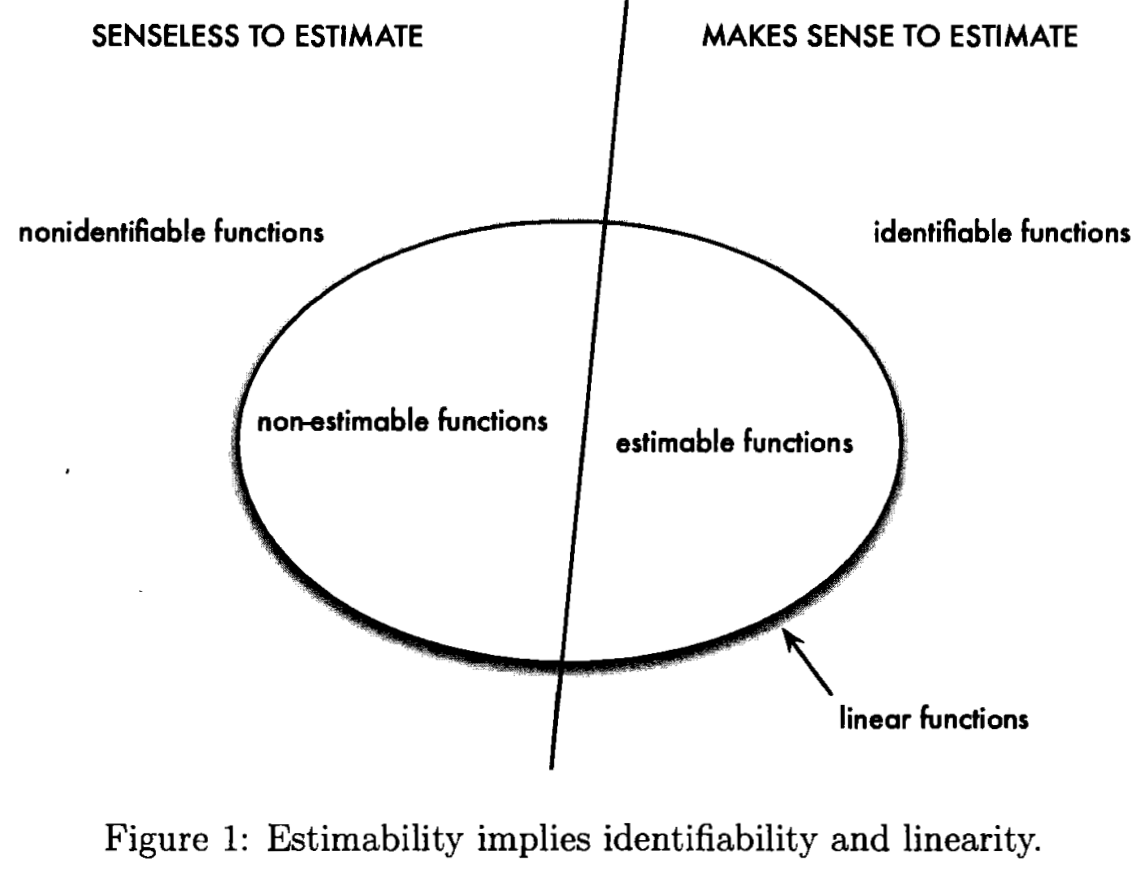
Informally, a parameterization is said to be identifiable if knowing $\bmu$ means knowing $\bbeta$.
Formally, the parameter $\bbeta$ is identifiable if $f(\bbeta_1)=f(\bbeta_2)$ implies that $\bbeta_1=\bbeta_2$ for any $\bbeta_1,\bbeta_2$.
More generally, the vector-valued function $g(\bbeta)$ is identifiable if $f(\bbeta_1)=f(\bbeta_2)$ implies that $g(\bbeta_1)=g(\bbeta_2)$.
In a linear model for which $X$ is full rank, $\bbeta$ is identifiable. But if $\X$ is not of full rank, there exist $\bbeta_1\neq \bbeta_2$ for which $\X\bbeta_1=\X\bbeta_2$.
A function $g(\bbeta)$ is identifiable iff $g(\bbeta)=(h\circ f)(\bbeta)$ for some function $h$. In particular, for OLMs, the only functions of the parameters that are identifiable are functions of $\X\bbeta$.
A linear function $\A\bbeta$ is called estimable if $\A\bbeta = \B\X\bbeta$ for some matrix $\B$. In other words, an estimable function is a linear function that is identifiable.