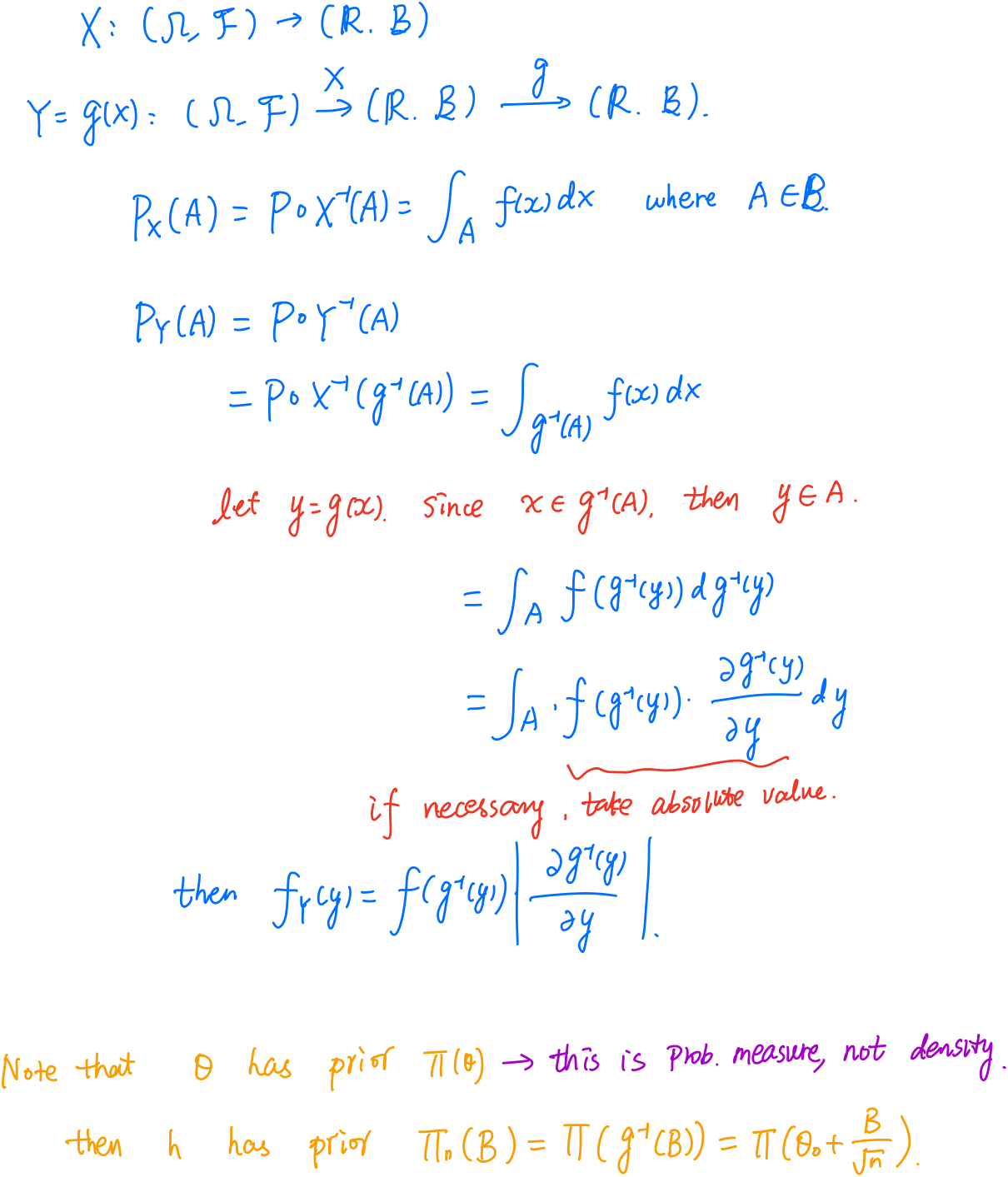Bernstein-von Mises Theorem
Posted on
I came across the Bernstein-von Mises theorem in Yuling Yao’s blog, and I also found a quick definition in the blog hosted by Prof. Andrew Gelman, although this one is not by Gelman. By coincidence, the former is the PhD student of the latter!
The quick definition said that
Under some conditions, a posterior distribution converges as you get more and more data to a multivariate normal distribution centred at the maximum likelihood estimator with covariance matrix given by $n^{-1}I(\theta_0)^{-1}$, where $\theta_0$ is the true population parameter.
The chapter 10 of Vaart (1998) presents more details of the theorem.
Before that, it discussed some intuitions behind the theorem. As we all known, the posterior density takes the form
\[p_{\Theta_n\mid X_1,\ldots, X_n}(\theta) = \frac{\prod_{i=1}^np_\theta(X_i)\pi(\theta)}{\int \prod_{i=1}^n p_\theta(X_i)\pi(\theta)d\theta}\,.\]If we rescale the parameter and study the sequence of posterior distributions $\sqrt n(\bar\Theta_n-\theta_0)$, whose densities are given by
\[p_{\sqrt n(\Theta_n - \theta_0)\mid X_1,\ldots, X_n}(\theta) = \frac{\prod_{i=1}^np_{\theta_0+h/\sqrt n}(X_i)\pi(\theta_0+h/\sqrt n)}{\int \prod_{i=1}^n p_{\theta_0+h/\sqrt n}(X_i)\pi(\theta_0+h/\sqrt n)dh}\,.\]If the prior density $\pi$ is continuous, then $\pi(\theta_0+h/\sqrt n)$ behaves like the constant $\pi(\theta_0)$ for large $n$, and $\pi$ cancels from the expression for the posterior density. For densities $p_\theta$ that are sufficiently smooth in the parameter, the sequence of models $(P_{\theta_0+h/\sqrt n}:h\in \IR^k)$ is locally asymptotically normal (TODO).
Formally,
Let the experiment $(P_\theta: \theta\in \Theta)$ be differentiable in quadratic mean at $\theta_0$ with nonsingular Fisher information matrix $I_{\theta_0}$, and suppose that for every $\varepsilon > 0$ there exists a sequence of tests $\phi_n$ such that
\begin{equation} P_{\theta_0}^n \phi_n\rightarrow 0,\sup_{\Vert \theta-\theta_0\Vert \ge \varepsilon} P_\theta^n(1-\phi_n)\rightarrow 0\,.\label{eq:assump} \end{equation}
Furthermore, let the prior measure be absolutely continuous in a neighborhood of $\theta_0$ with a continuous positive density at $\theta_0$. Then the corresponding posterior distributions satisfy
\[\left\Vert P_{\sqrt n(\bar\Theta_n-\theta_0)\mid X_1,\ldots,X_n} - N(\Delta_{n,\theta_0}, I_{\theta_0}^{-1}) \right\Vert\overset{P_{\theta_0}^n}{\rightarrow}0\,,\]where
\[\Delta_{n,\theta_0} = \frac{1}{\sqrt n}\sum_{i=1}^n I_{\theta_0}^{-1}\dot\ell_{\theta_0}(X_i)\,.\]
\eqref{eq:assump} means that there exists a sequence of uniformly consistent tests for testing $H_0:\theta=\theta_0$ against $H_1:\Vert \theta-\theta_0\Vert\ge \varepsilon$ for every $\varepsilon > 0$. In other words, it must be possible to separate the true value $\theta_0$ from the complements of balls centered at $\theta_0$.
Change of variables
The proof rescales the parameter $\theta$ to the parameter $\theta$ to the local parameter $h = \sqrt n(\theta - \theta_0)$, then the corresponding prior distribution on $h$ is $\Pi_n(B)=\Pi(\theta_0+B/\sqrt n)$, where $\Pi$ is the probability measure of the prior distribution on $\theta$.
Note that both $\Pi_n$ and $\Pi$ are probability measure, not the probability density. And it reminds me to review the relationship between Jacobian transformation and the change of measure. Here is my loose derivation.