Bootstrap Sampling Distribution

Posted on Mar 05, 2020

Tags: Bootstrap, Permutation Test

This note is based on Lehmann, E. L., & Romano, J. P. (2005). Testing statistical hypotheses (3rd ed). Springer.

Let $X^n = (X_1,\ldots, X_n)$ be a sample of $n$ i.i.d. random variables taking values in a sample space $S$ and having unknown probability distribution $P\in \cP$. The interest is to infer some parameter $\theta(P)$. Denote $\Theta = \{\theta(P):P\in\cP\}$ be the range of $\theta$.

Consider a term called root, $R_n(X^n, \theta(P))$, which is just some real-valued functional depending on both $X^n$ and $\theta(P)$. The idea is that a CI for $\theta(P)$ could be constructed if the distribution of the root were known.

If the problem is nonparametric, a natural construction for an estimator $\hat\theta_n$ of $\theta(P)$ is the plug-in estimator $\hat\theta_n=\theta(\hat P_n)$, where $\hat P_n$ is the empirical distribution of the data,

\[\hat P_n(E) = \frac 1n\sum_{i=1}^nI\{X_i\in E\}\,.\]

For parametric problem, i.e., $\cP = \{P_\psi:\psi\in \Psi\}$, then $\theta(P)$ can be described as a functional $t(\psi)$, and hence $\hat\theta_n$ is often taken to be $t(\hat\psi_n)$, where $\hat\psi_n$ is some desirable estimator of $\psi$.

Let $J_n(P)$ be the distribution of $R_n(X^n, \theta(P))$ under $P$, and let $J_n(\cdot, P)$ be the corresponding CDF defined by

\[J_n(x, P) = P\{R_n(X^n, \theta(P))\le x\}\,.\]

The bootstrap procedure is a general, direct approach to approximate the sampling distribution $J_n(P)$ by $J_n(\hat P_n)$, where $\hat P_n$ is an estimate of $P$ in $\cP$. In this light, the bootstrap estimate $J_n(\hat P_n)$ is a simple plug-in estimate of $J_n(P)$.

• in parametric estimation, $\hat P_n$ maybe $P_{\hat \psi_n}$
• in nonparametric estimation, $\hat P_n$ is typically the empirical distribution

In order to get around the non-continuity and non-strictly-increasing problem, define

\[J_n^{-1} = \inf\{x:J_n(x,P)\ge 1-\alpha\}\,,\]

then if $J_n(\cdot, P)$ has a unique quantile $J_n^{-1}(1-\alpha, P)$,

\[P(R_n(X^n, \theta(P))\le J_n^{-1}(1-\alpha, P)) = 1-\alpha\,.\]

The resulting bootstrap CI for $\theta(P)$ of nominal level $1-\alpha$ could be

\[\{\theta\in \Theta:R_n(X^n,\theta) \le J_n^{-1}(1-\alpha, \hat P_n)\}\]

or

\[\{\theta\in \Theta:J_n^{-1}(\alpha/2, \hat P_n)\le R_n(X^n,\theta) \le J_n^{-1}(1-\alpha/2, \hat P_n)\}\]

Outside certain exceptional cases (TODO), the bootstrap approximation $J_n(x,\hat P_n)$ cannot be calculated exactly. Typically, we resort to a Monte Carlo approximation to $J_n(P)$, conditional on the data $X^n$, for $j=1,\ldots,B$, let $X_j^{n*}$ be a sample of $n$ i.i.d. observation from $\hat P_n$, which is also referred to as the $j$-th bootstrap sample of size $n$. When $\hat P_n$ is the empirical distribution, this amounts to resampling the original observations with replacement.

Consider the consistency of the bootstrap estimator $J_n(\hat P_n)$ of the true sampling distribution $J_n(P)$ of $R_n(X^n,\theta(P))$. For the bootstrap to be consistent, $J_n(P)$ must be smooth in $P$ since we are replacing $P$ by $\hat P_n$.

Parametric Bootstrap

Suppose $X^n=(X_1,\ldots, X_n)$ is a sample from a q.m.d. model $\{P_\theta,\theta\in \Omega\}$.

The family $\{P_\theta,\theta\in \Omega\}$ is quadratic mean differentiable (q.m.d.) at $\theta_0$ if there exists a vector of real-valued functions $\eta(\cdot,\theta_0) = (\eta_1(\cdot,\theta_0),\ldots,\eta_k(\cdot,\theta_0))^T$ such that

\[\int_\cX\left[\sqrt{p_{\theta_0+h}(x)} -\sqrt{p_{\theta_0}(x)}-\langle \eta(x,\theta_0),h\rangle\right]^2d\mu(x) = o(\vert h\vert^2)\]

as $\vert h\vert\rightarrow 0$.

Suppose $\hat \theta_n$ is an efficient likelihood estimator in the sense that

\[n^{1/2}(\hat\theta_n-\theta_0) = I^{-1}(\theta_0)Z_n + o_{P_{\theta_0}^n}(1)\,,\]

where $Z_n$ is the normalized score vector

\[Z_n = Z_n(\theta_0) = 2n^{-1/2}\sum_{i=1}^n[\eta(X_i,\theta_0)/p_{\theta_0}^{1/2}(X_i)]\,.\]

Suppose $g(\theta)$ is a differentiable map from $\Omega$ to $\IR$ with nonzero graident vector $\dot g(\theta)$. Consider the root $R_n(X^n,\theta) = n^{1/2}[g(\hat\theta_n)-g(\theta)]$, with distribution function $J_n(x,\theta)$. It can show that

\[J_n(x,\theta)\rightarrow N(0, \dot g(\theta)I^{-1}(\theta)\dot g(\theta)^T) \triangleq N(0, \sigma_\theta^2)\,.\]

It may difficult to calculate the limiting variance $\sigma_\theta^2$, then one can use the approximation

\[\hat\sigma_n^2 = \dot g(\hat\theta_n) I^{-1}(\hat\theta_n)\dot g(\hat \theta_n)^T\,,\]

which can be poor. Then we can consider bootstrap method, use the approximation $J_n(x,\hat\theta_n)$, which is differ from the above $\widehat{\lim J_n(x,\theta)}$.

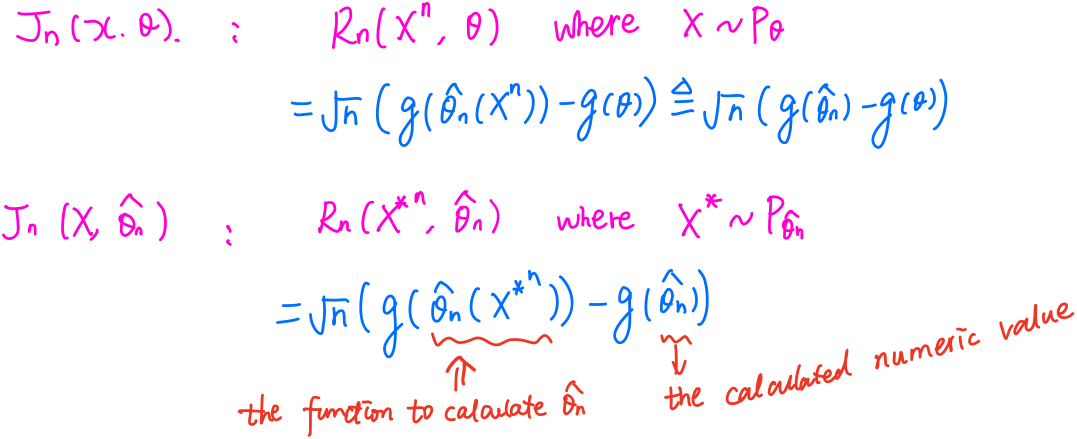
Let $X_1,\ldots, X_n$ be i.i.d. random variables with pdf $\frac 1\sigma f(\frac{x-\mu}{\sigma})$, where $f$ is a known Lebesgue pdf and $\mu,\sigma$ are unknown. Let $X_1^*,\ldots, X_n^*$ be i.i.d. bootstrap data from the pdf $\frac 1s f(\frac{x-\bar x}{s})$, where $\bar x$ and $s^2$ are the observed sample mean and sample variance, respectively.

Comparison with Permutation Test

In the introduction of the section of Bootstrap method in Lehmann & Romano (2005), it said,

In the previous section, it was shown how permutation and randomization tests can be used in certain problems where the randomization hypothesis holds. Unfortunately, randomization tests only apply to a restricted class of problems. In this section, we discuss some generally used asymptotic approaches for constructing confidence regions or hypothesis tests.

So it sounds like the bootstrap procedure is more general than the permutation test, but I have not read the section about permutation test (TODO). Here I try to compare them in terms of test statistic.

To compare two group means with $\sigma_1=\sigma_2$, a natural test statistic is

\[t = \bar x_2 - \bar x_1\,.\]

(here the denominator $se$ is omitted) In the permutation test, we propose

\[t^*_p = \bar x_2^{*p} - \bar x_1^{*p} \,,\]

while

\[t^*_b = (\bar x_2^{*b} - \bar x_2)- (\bar x_1^{*b} -\bar x_1)\]

for bootstrap procedure, and the observations in the permutation test are sampled without replacement, while the observations in the bootstrap test are sampled with replacement. Detailed example can be found in bootstrap test for eigenfunctions and permutation test for gene.

More deep comparison with permutation test can be found in the one year ago’s post. I feel very guilty, I didn’t realize that I wrote such staff until I found there are two posts has the “bootstrap” tag.