The Gibbs Sampler
Posted on (Update: )
Gibbs sampler is an iterative algorithm that constructs a dependent sequence of parameter values whose distribution converges to the target joint posterior distribution.
A semiconjugate prior distribution
In the case where $\tau_0^2$ is not proportional to $\sigma^2$, the marginal density of $1/\sigma^2$ is not a gamma distribution.
Discrete approximations
A discrete approximation to the posterior distribution makes use of these facts by constructing a posterior distribution over a grid of parameter values, based on relative posterior probabilities.
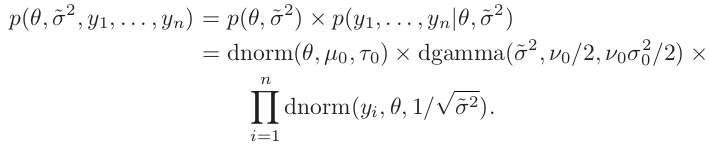
Construct a two-dimensional grid of value of ${\theta, \tilde \sigma^2}$
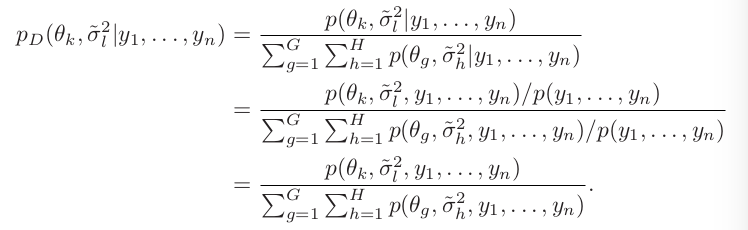
An example
mu0 = 1.9; t20 = 0.95^2; s20 = 0.01; nu0 = 1
y = c(1.64, 1.70, 1.72, 1.74, 1.82, 1.82, 1.82, 1.90, 2.08)
G = 100; H = 100
mean.grid = seq(1.505, 2.00, length = G)
prec.grid = seq(1.75,175, length = H)
post.grid = matrix(nrow = G, ncol = H)
for (g in 1:G){
for (h in 1:H){
post.grid[g, h] =
dnorm(mean.grid[g], mu0, sqrt(t20)) *
dgamma(prec.grid[h], nu0/2, s20*nu20/2) *
prod(dnorm(y, mean.grid[g], 1/sqrt(prec.grid[h])))
}
}
post.grid = post.grid/sum(post.grid)
Sampling from the conditional distributions
if we know $\theta$, we can easily sample directly from $p(\sigma^2\mid \theta,y_1,\ldots,y_n)$. And we can easily sample from $p(\theta\mid\sigma^2,y_1,\ldots,y_n)$.
-
suppose we sample from the marginal posterior distribution $p(\sigma^2\mid y_1,\ldots, y_n)$ and obtain $\sigma^{2(1)}$.
-
then we could sample $\theta^{(1)}\sim p(\theta\mid \sigma^{2(1)},y_1,\ldots,y_n)$, and {$\theta^{(1)},\sigma^{2(1)}$} would be a sample from the joint distribution of {$\theta,\sigma^2$}.
-
$\theta^{(1)}$ could be considered a sample from the marginal distribution $p(\theta\mid y_1,\ldots,y_n)$. For this $\theta$-value, sample $\sigma^{(2)}\sim p(\sigma^2\mid \theta^{(1)},y_1,\ldots,y_n)$
-
{$\theta^{(1)},\sigma^{2(2)}$} is also a sample from the joint distribution of {$\theta,\sigma^2$}. This in turn means that $\sigma^{2(2)}$ is a sample from the marginal distribution $p(\sigma^2\mid y_1,\ldots,y_n)$, which then could be used to generate a new sample $\theta^{(2)}$.
Gibbs sampling
the full conditional distributions \(p(\theta\mid \sigma^2,y_1,\ldots,y_n)\) and \(p(\sigma^2\mid \theta,y_1,\ldots,y_n)\)
given a current state of the parameters \(\phi^{(s)}=\{\theta^{(s)}, \tilde \sigma^{2(s)}\}\)
generate a new state as follows
- sample $\theta^{(s+1)}\sim p(\theta\mid \tilde\sigma^{2(s)},y_1,\ldots,y_n)$
- sample $\tilde\sigma^{2(s+1)}\sim p(\tilde\sigma^2\mid \theta^{(s+1)},y_1,\ldots,y_n)$
- let $\phi^{(s+1)}={\theta^{s+1},\tilde\sigma^{2(s+1)}}$
General properties of the Gibbs sampler
Markov property, Markov chain.
\[\Pr(\phi^{(s)}\in A)\rightarrow \int_A p(\phi)d\phi\;as\;s\rightarrow \infty\]the sampling distribution of $\phi^{(s)}$ approaches the target distribution as $s \rightarrow \infty $, no matter what the starting value $\phi^{(0)}$ is (although some starting values will get you to the target sooner than others).
More importantly, for most functions $g$ of interest,
\[\frac{1}{S}\sum\limits_{s=1}^Sg(\phi^{(s)})\rightarrow E(g(\phi))=\int g(\phi)p(\phi)d\phi\;as\;S\rightarrow \infty\]the necessary ingredients of a Bayesian data analysis are
- Model specification: $p(y\mid \phi)$
- Prior specification: $p(\phi)$
- Posterior summary: $p(\phi\mid y)$
Remarks:
Monte Carlo and MCMC sampling algorithms
- are not models
- do not generate “more information” than is in $y$ and $p(\phi)$
- simply “ways of looking at” $p(\phi\mid y)$
for example,
\[\frac{1}{S}\sum\phi^{(s)}\approx \int\phi p(\phi\mid y)d\phi\] \[\frac{1}{S}1(\phi^{(s)}\le c)\approx Pr(\phi\le c\mid y)=\int_{-\infty}^cp(\phi\mid y)d\phi\]Distinguishing parameter estimation from posterior approximation
Introduction to MCMC diagnostics
difference between MC and MCMC
- Independent MC samples automatically create a sequence that is representative of $p(\phi)$: The probability that $\phi\in A$ for any set $A$ is $\int_A p(\phi) d\phi$. This is true for every $s \in {1, . . . , S}$ and conditionally or unconditionally on the other values in the sequence.
- NOT true for MCMC, instead we have
Two types of Gibbs sampler
Suppose we can decompose the random variable into $d$ components, $\mathbf x=(x_1,\ldots, x_d)$. In the Gibbs sampler, one randomly or symmetrically chooses a coordinate, say $x_1$, then updates it with new sample $x_1’$ draw from the conditional distribution $\pi(\cdot\mid \mathbf x_{[-1]})$.
Random-scan Gibbs Sampler
Let $\mathbf x^{(t)}=(x_1^{(t)},\ldots, x_d^{(t)})$ for iteration $t$. Then, at iteration $t+1$, conduct the following steps:
- Randomly select a coordinate $i$ from ${1, \ldots, d}$ according to a given probability vector $(\alpha_1, \ldots, \alpha_d)$
- Draw $x_{i}^{(t+1)}$ from the conditional distribution $\pi(\cdot\mid x_{[-i]}^{(t)})$ and leave the remaining components unchanged
Systematic-Scan Gibbs Sampler
Let $\mathbf x^{(t)}=(x_1^{(t)},\ldots, x_d^{(t)})$ for iteration $t$. Then, at iteration $t+1$,
- Draw $x_i^{i+1}$ from the conditional distribution
In the both samplers, at every update step, $\pi$ is still invariant. Suppose $\mathbf x^{(t)}\sim \pi$, then $\mathbf x_{[-i]}^{(t)}$ follows its marginal distribution under $\pi$. Thus,
\[\pi(x_i^{(t+1)}\mid \mathbf x_{[-i]}^{(t)})\times \pi(\mathbf x_{[-i]}^{(t)}) = \pi(\mathbf x_{[-i]}^{(t)}, x_i^{(t+1)})\]which means that after one conditional update, the new configuration still follows distribution $\pi$.