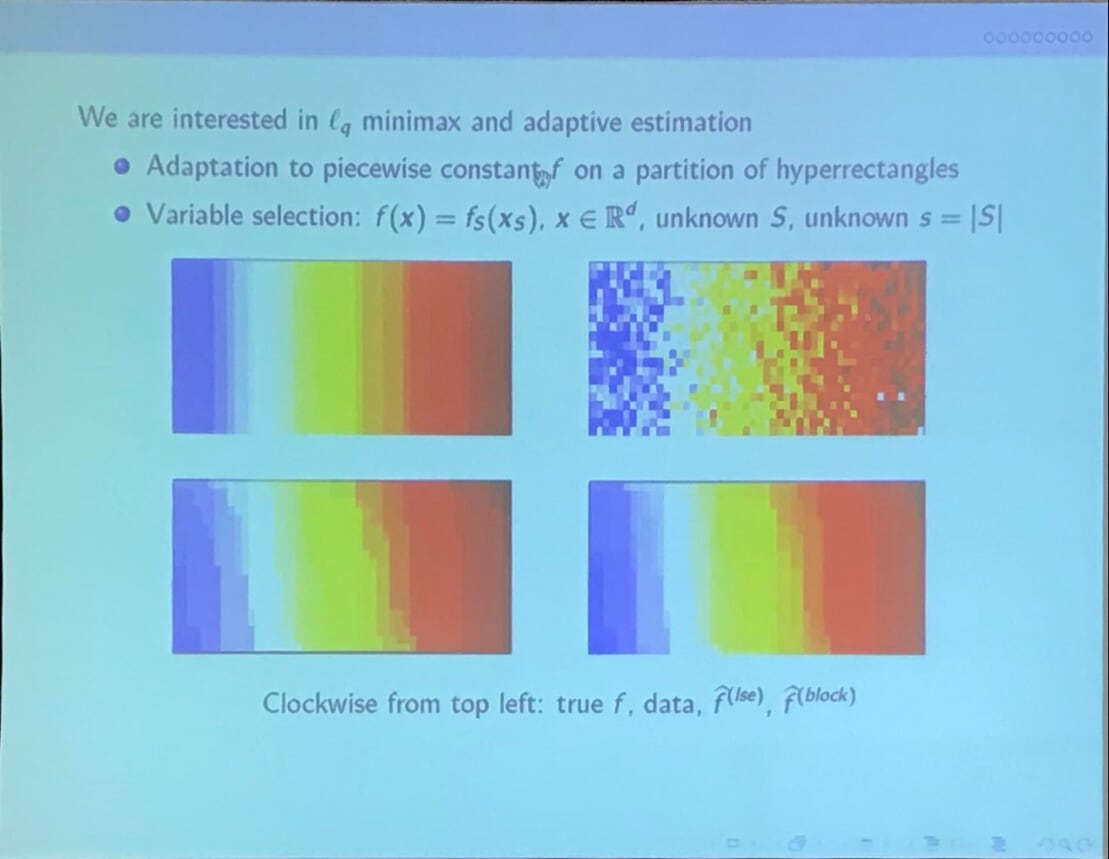
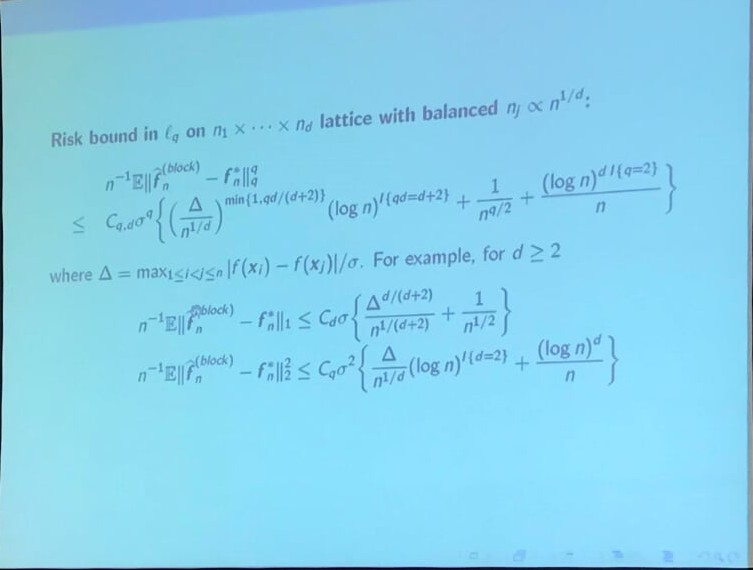Multiple Isotonic Regression
Posted on
The first two sections are based on a good tutorial on the isotonic regression, and the third section consists of the slides for the talk given by Prof. Cun-Hui Zhang at the 11th ICSA International Conference on Dec. 21st, 2019.
Isotonic Regression
Intuitionally, linear ordering isotonic regression can be thought as approximating given series of 1-dimensional observations with non-decreasing function, while general isotonic regression is approximating given series of values which satisfy a given partial ordering.
Formally, given values $\mathbf{a}\in \IR^n$ and the associated positive weights $\w\in\IR^n > 0$,
\[\begin{align*} \min_\y& \sum_{i=1}^nw_i(y_i-a_i)^2\\ \st & y_i\ge y_j\; \forall (i,j) \in E \end{align*}\]where the set of constraints $E$ constitutes a acyclic graph.
In particular, the aforementioned linear ordering isotonic regression is one with constraint $y_1\le y_2\le\ldots\le y_n$. There is a simple linear algorithm for such special case, called Pool Adjacent Violators Algorithm (PAVA).
Pool Adjacent Violators Algorithm
For an optimal solution, if $a_i \ge a_{i+1}$, then $y_i = y_{i+1}$.
It is quite clear from the following sketch,
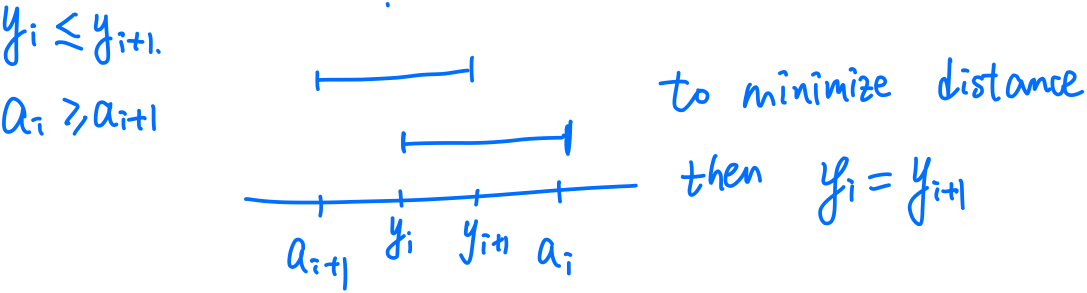
Formally, we can prove it by contradiction, i.e., suppose $y_i < y_{i+1}$, then

Since $y_i = y_{i+1}$, we can combine $(w_i, a_i)$ and $(w_{i+1}, a_{i+1})$ as a new point,
\[(w_i+w_{i+1}, \frac{w_ia_i+w_{i+1}a_{i+1}}{w_i+w_{i+1}})\,.\]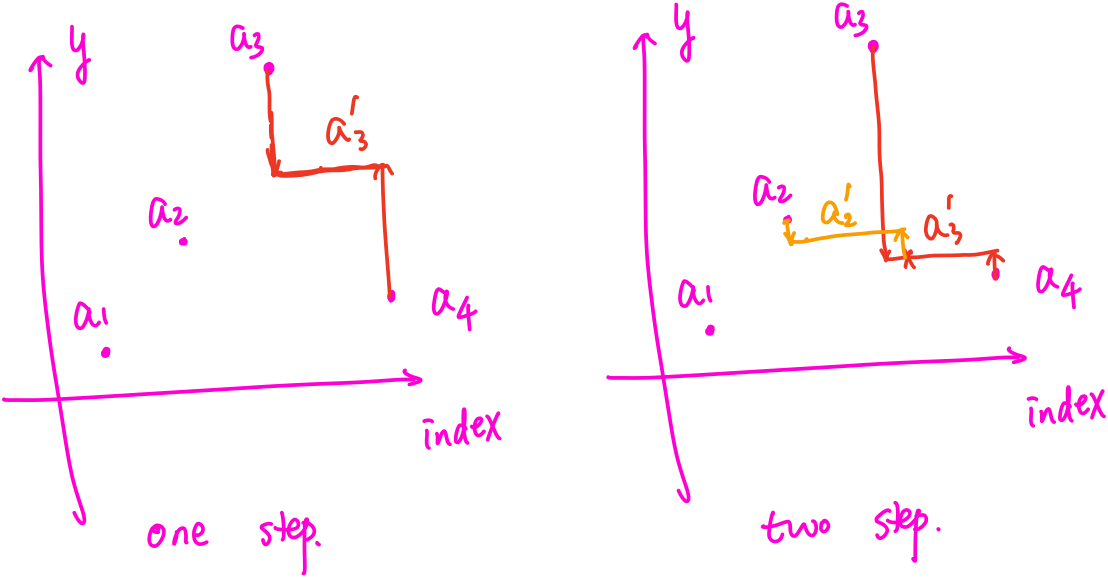
Repeating the combining procedure until the value $a_i’ <= a_{i+1}’$, and then the solution exactly equals to the corresponding combined point.
Actually, I had implemented the PAVA for a toy example in R and Julia, but I forgot completely (my guilt).
Multiple Isotonic Regression

Pay attention to the notation difference, we can treat $y_i, \x_i$ in the slide as $a_i, y_i$ in the previous section, respectively. And there is one more additional non-decreasing function $f$. More formal description can be found in their paper,