Estimate Parameters in Logistic Regression
Posted on
Background
Assuming $\boldsymbol y$ is a $n\times 1$ response variable, and $y_i\sim B(1, \pi_i)$. $\boldsymbol x_1,\ldots,\boldsymbol x_p$ are $p$ explanatory variables.
Then the likelihood of $\boldsymbol y$ is
\[L(\pi_1,\ldots,\pi_n)=\prod\limits_{i=1}^n\pi_i^{y_i}(1-\pi_i)^{1-y_i}\]and the log-likelihood is
\[l(\pi_1,\ldots,\pi_n)=\sum\limits_{i=1}^n[y_i\log\pi_i+(1-y_i)\log(1-\pi_i))]\]The logistic regression said that
\[y_i=\logit(\pi_i) = \log\frac{\pi_i}{1-\pi_i}=\boldsymbol x_i'\boldsymbol\beta\]where
\[\boldsymbol\beta = (\beta_0,\beta_1,\ldots,\beta_p)\qquad \boldsymbol x_i = (1, x_{i1}, \ldots, x_{ip})'\]then we have
\[\pi_i = \frac{\exp(\boldsymbol x_i'\boldsymbol\beta)}{1+\exp(\boldsymbol x_i'\boldsymbol\beta)}\]Thus, the log-likelihood could be
\[l(\boldsymbol{\beta})=\sum\limits_{i=1}^n[y_i\boldsymbol {x_i'}\boldsymbol{\beta}-\log(1+\exp(\boldsymbol {x_i'}\boldsymbol{\beta}))]\]Maximum Likelihood Estimate
We need to find $\boldsymbol \beta$ to minimize $l(\boldsymbol \beta)$, which means that
\[\frac{\partial l(\boldsymbol \beta)}{\partial \boldsymbol \beta}=\sum\limits_{i=1}^n(y_i-\frac{\exp(\boldsymbol {x_i'}\boldsymbol{\beta})}{1+\exp(\boldsymbol x_i'\boldsymbol\beta)})\boldsymbol x_i = 0\]We adopt Newton-Raphson Algorithm (Multivariate version) to solve $\boldsymbol \beta$ numerically.
Let
\[f_j(\boldsymbol \beta) = \sum\limits_{i=1}^n(y_i-\frac{\exp(\boldsymbol x_i'\boldsymbol\beta)}{1+\exp(\boldsymbol x_i'\boldsymbol\beta)})\boldsymbol x_{ij} = 0\]then
\[\frac{\partial l(\boldsymbol \beta)}{\partial \boldsymbol \beta} = \boldsymbol f=(f_0,\ldots, f_p)\]so
\[\boldsymbol J = \left[ \begin{array}{cccc} \frac{\partial f_0}{\partial \beta_0} & \frac{\partial f_0}{\partial \beta_1} & \cdots & \frac{\partial f_0}{\partial \beta_p}\\ \frac{\partial f_1}{\partial \beta_0} & \frac{\partial f_1}{\partial \beta_1} & \cdots & \frac{\partial f_1}{\partial \beta_p}\\ \vdots & \vdots & \ddots & \vdots\\ \frac{\partial f_p}{\partial \beta_0} & \frac{\partial f_p}{\partial \beta_1} & \cdots & \frac{\partial f_p}{\partial \beta_p}\\ \end{array} \right]\]where
\[\frac{\partial f_j}{\partial \beta_k} = -\sum\limits_{i=1}^n(1-\pi_i)\pi_ix_{ij}x_{ik}\]The Newton-Raphson formula for multi-variate problem is
\[\boldsymbol \beta = \boldsymbol \beta - J^{-1}(\boldsymbol \beta)\boldsymbol f(\boldsymbol \beta)\]Wald Test for Parameters
In the univariate case, the Wald statistic is
\[\frac{(\hat \theta-\theta_0)}{var(\hat\theta)}\]which is compared against a chi-squared distribution.
Alternatively, the difference can be compared to a normal distribution. In this case, the test statistic is
\[\frac{\hat\theta-\theta_0}{se(\hat\theta)}\]where $se(\hat\theta)$ is the standard error of the maximum likelihood estimate. Assuming $\mathbf H$ is the Hessian of the log-likelihood function $l$, then the vector $\sqrt{diag((-\mathbf H)^{-1})}$ is the estimate of the standard error of each parameter value at its maximum.
Implement in C++ and R
Implement above algorithm and apply to an example, and compare the logistic regression results with glm(..., family = binomial()) in R.
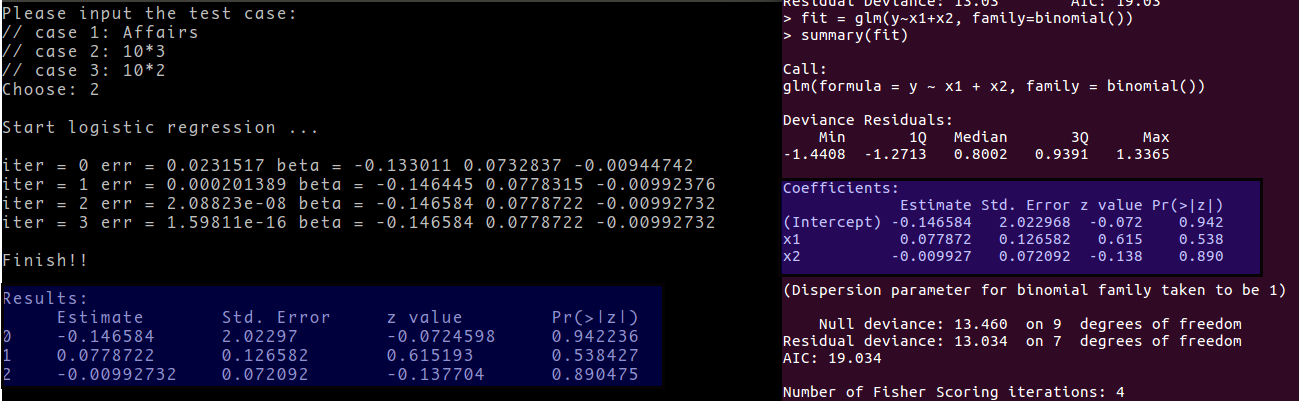
If you want to know more details, you can visit my github repository gsl_lm/logit.